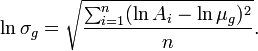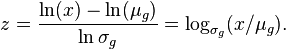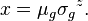Geometric standard deviation
In probability theory and statistics, the geometric standard deviation describes how spread out are a set of numbers whose preferred average is the geometric mean. For such data, it may be preferred to the more usual standard deviation. Note that unlike the usual arithmetic standard deviation, the geometric standard deviation is a multiplicative factor, and thus is dimensionless, rather than having the same dimension as the input values.
Definition
If the geometric mean of a set of numbers {A1, A2, ..., An} is denoted as μg, then the geometric standard deviation is
Derivation
If the geometric mean is
then taking the natural logarithm of both sides results in
The logarithm of a product is a sum of logarithms (assuming  is positive for all
is positive for all  ), so
), so
It can now be seen that  is the arithmetic mean of the set
is the arithmetic mean of the set 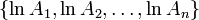 , therefore the arithmetic standard deviation of this same set should be
, therefore the arithmetic standard deviation of this same set should be
This simplifies to
Geometric standard score
The geometric version of the standard score is
If the geometric mean, standard deviation, and z-score of a datum are known, then the raw score can be reconstructed by
Relationship to log-normal distribution
The geometric standard deviation is related to the log-normal distribution. The log-normal distribution is a distribution which is normal for the logarithm transformed values. By a simple set of logarithm transformations we see that the geometric standard deviation is the exponentiated value of the standard deviation of the log transformed values (e.g. exp(stdev(ln(A))));
As such, the geometric mean and the geometric standard deviation of a sample of data from a log-normally distributed population may be used to find the bounds of confidence intervals analogously to the way the arithmetic mean and standard deviation are used to bound confidence intervals for a normal distribution. See discussion in log-normal distribution for details.
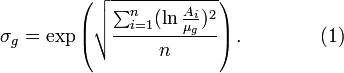
![\mu _{g}={\sqrt[ {n}]{A_{1}A_{2}\cdots A_{n}}}.\,](/2014-wikipedia_en_all_02_2014/I/media/c/0/8/1/c0816739d94c66c564be962b99fa14bb.png)

![\ln \mu _{g}={1 \over n}[\ln A_{1}+\ln A_{2}+\cdots +\ln A_{n}].\,](/2014-wikipedia_en_all_02_2014/I/media/2/d/2/2/2d221f9bc9446c07a12bcafc93a358ff.png)