Geodesic curvature

From Wikipedia, the free encyclopedia

In Riemannian geometry, the geodesic curvature $k_{g}$ of a curve $\gamma$ measures how far the curve is from being a geodesic. In a given manifold ${\bar {M}}$ , the geodesic curvature is just the usual curvature of $\gamma$ (see below), but when $\gamma$ is restricted to lie on a submanifold $M$ of ${\bar {M}}$ (e.g. for curves on surfaces), geodesic curvature refers to the curvature of $\gamma$ in $M$ and it is different in general from the curvature of $\gamma$ in the ambient manifold ${\bar {M}}$ . 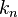The (ambient) curvature $k$ of $\gamma$ depends on two factors: the curvature of the submanifold $M$ in the direction of $\gamma$ (the normal curvature $k_{n}$ ), which depends only from the direction of the curve, and the curvature of $\gamma$ seen in $M$ (the geodesic curvature $k_{g}$ ), which is a second order quantity. The relation between these is $k={\sqrt {k_{g}^{2}+k_{n}^{2}}}$ . 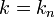In particular geodesics on $M$ have zero geodesic curvature (they are "straight"), so that $k=k_{n}$ , which explains why they appear to be curved in ambient space whenever the submanifold is.

Definition

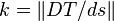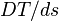Consider a curve $\gamma$ in a manifold ${\bar {M}}$ , parametrized by arclength, with unit tangent vector $T=d\gamma /ds$ . Its curvature is the norm of the covariant derivative of $T$ : $k=\|DT/ds\|$ . If $\gamma$ lies on $M$ , the geodesic curvature is the norm of the projection of the covariant derivative $DT/ds$ on the tangent space to the submanifold. Conversely the normal curvature is the norm of the projection of 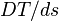$DT/ds$ on the normal bundle to the submanifold at the point considered.

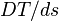If the ambient manifold is the euclidean space ${\mathbb {R}}^{n}$ , then the covariant derivative $DT/ds$ is just the usual derivative $dT/ds$ .

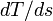Example

Let $M$ be the unit sphere $S^{2}$ in three dimensional Euclidean space. The normal curvature of $S^{2}$ is identically 1, independently of the direction considered. Great circles have curvature $k=1$ , so they have zero geodesic curvature, and are therefore geodesics. Smaller circles of radius $r$ will have curvature $1/r$ and geodesic curvature $k_{g}={\sqrt {1-r^{2}}}/r$ .

Some results involving geodesic curvature

The geodesic curvature is no other than the usual curvature of the curve when computed intrinsically in the submanifold $M$ . It does not depend on the way the submanifold $M$ sits in ${\bar {M}}$ .

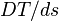Geodesics of $M$ have zero geodesic curvature, which is equivalent to saying that $DT/ds$ is orthogonal to the tangent space to $M$ .

On the other hand the normal curvature depends strongly on how the submanifold lies in the ambient space, but marginally on the curve: 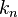$k_{n}$ only depends on the point on the submanifold and the direction $T$ , but not on $DT/ds$ .

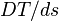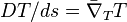In general Riemannian geometry, the derivative is computed using the Levi-Civita connection ${\bar {\nabla }}$ of the ambient manifold: $DT/ds={\bar {\nabla }}_{T}T$ . It splits into a tangent part and a normal part to the submanifold: 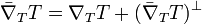${\bar {\nabla }}_{T}T=\nabla _{T}T+({\bar {\nabla }}_{T}T)^{\perp }$ . 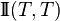The tangent part is the usual derivative $\nabla _{T}T$ in $M$ (it is a particular case of Gauss equation in the Gauss-Codazzi equations), while the normal part is ${\mathrm {I\!I}}(T,T)$ , where ${\mathrm {I\!I}}$ denotes the second fundamental form.

The Gauss–Bonnet theorem.

References

do Carmo, Manfredo P. (1976), Differential Geometry of Curves and Surfaces, Prentice-Hall, ISBN 0-13-212589-7
Guggenheimer, Heinrich (1977), "Surfaces", Differential Geometry, Dover, ISBN 0-486-63433-7 .
Slobodyan, Yu.S. (2001), "Geodesic curvature", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 .

External links

Weisstein, Eric W., "Geodesic curvature", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.