Gentzen's consistency proof
Gentzen's consistency proof is a result of proof theory in mathematical logic. It "reduces" the consistency of a simplified part of mathematics, not to something that could be proved in that same simplified part of mathematics (which would contradict the basic results of Kurt Gödel), but rather to a simpler logical principle.
Gentzen's theorem
In 1936 Gerhard Gentzen proved the consistency of first-order arithmetic using combinatorial methods. Gentzen's proof shows much more than merely that first-order arithmetic is consistent. Gentzen showed that the consistency of first-order arithmetic is provable, over the base theory of primitive recursive arithmetic with the additional principle of quantifier-free transfinite induction up to the ordinal ε0. Informally, this additional principle means that there is a well-ordering on the set of finite rooted trees.
The principle of quantifier-free transfinite induction up to ε0 says that for any formula A(x) with no bound variables transfinite induction up to ε0 holds. ε0 is the first ordinal  , such that
, such that 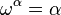 , i.e. the limit of the sequence:
, i.e. the limit of the sequence:
To express ordinals in the language of arithmetic an ordinal notation is needed, i.e. a way to assign natural numbers to ordinals less than ε0. This can be done in various ways, one example provided by Cantor's normal form theorem. That transfinite induction holds for a formula A(x) means that A does not define an infinite descending sequence of ordinals smaller than ε0 (in which case ε0 would not be well-ordered). Gentzen assigned ordinals smaller than ε0 to proofs in first-order arithmetic and showed that if there is a proof of contradiction, then there is an infinite descending sequence of ordinals < ε0 produced by a primitive recursive operation on proofs corresponding to a quantifier-free formula.
Relation to Gödel's theorem
Gentzen's proof also highlights one commonly missed aspect of Gödel's second incompleteness theorem. It is sometimes claimed that the consistency of a theory can only be proved in a stronger theory. The theory obtained by adding quantifier-free transfinite induction to primitive recursive arithmetic proves the consistency of first-order arithmetic but is not stronger than first-order arithmetic. For example, it does not prove ordinary mathematical induction for all formulae, while first-order arithmetic does (it has this as an axiom schema). The resulting theory is not weaker than first-order arithmetic either, since it can prove a number-theoretical fact - the consistency of first-order arithmetic - that first-order arithmetic cannot. The two theories are simply incomparable.
Gentzen's proof is the first example of what is called proof-theoretical ordinal analysis. In ordinal analysis one gauges the strength of theories by measuring how large the (constructive) ordinals are that can be proven to be well-ordered, or equivalently for how large a (constructive) ordinal can transfinite induction be proven. A constructive ordinal is the order type of a recursive well-ordering of natural numbers.
Laurence Kirby and Jeff Paris proved in 1982 that Goodstein's theorem cannot be proven in Peano arithmetic based on Gentzen's theorem.
References
- Gentzen, Gerhard (1936), "Die Widerspruchsfreiheit der reinen Zahlentheorie", Mathematische Annalen 112: 493–565, doi:10.1007/BF01565428 - Translated as 'The consistency of arithmetic', in (Gentzen & Szabo 1969).
- Gentzen, Gerhard (1938), "Neue Fassung des Widerspruchsfreiheitsbeweises für die reine Zahlentheorie", Forschungen zur Logik und zur Grundlegung der exakten Wissenschaften 4: 19–44 - Translated as 'New version of the consistency proof for elementary number theory', in (Gentzen & Szabo 1969).
- Gentzen, Gerhard (1969), M. E., Szabo, ed., Collected Papers of Gerhard Gentzen, Studies in logic and the foundations of mathematics (Hardcover ed.), Amsterdam: North-Holland, ISBN 0-7204-2254-X - an English translation of papers.
- Gödel, K. (2001) [1938], "Lecture at Zilsel’s", in Feferman, Solomon, Kurt Gödel: Collected Works, vol.III Unpublished Essays and Lectures (Paperback ed.), Oxford University Press Inc., pp. 87–113, ISBN 0-19-514722-7
- Jervell, Herman Ruge (1999), A course in proof theory (textbook draft ed.)
- Kirby, L.; Paris, J. (1982), "Accessible independence results for Peano arithmetic" (PDF), Bull. London Math. Soc. (LMS) 14: 285–293
- Tait, W. W. (2005), "Gödel's reformulation of Gentzen's first consistency proof for arithmetic: the no-counterexample interpretation" (PDF), The Bulletin of Symbolic Logic (ASL) 11 (2): 225–238, ISSN 1079-8986