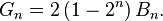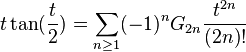Genocchi number

From Wikipedia, the free encyclopedia

In mathematics, the Genocchi numbers G_n, named after Angelo Genocchi, are a sequence of integers that satisfy the relation

${\frac {2t}{e^{t}+1}}=\sum _{{n=1}}^{{\infty }}G_{n}{\frac {t^{n}}{n!}}.$

The first few Genocchi numbers are 1, −1, 0, 1, 0, −3, 0, 17 (sequence A001469 in OEIS).

Properties

The generating function definition of the Genocchi numbers implies that they are rational numbers. In fact, G_2n+1 = 0 for n ≥ 1 and (−1)ⁿG_2n is an odd positive integer.

Genocchi numbers G_n are related to Bernoulli numbers B_n by the formula

$G_{n}=2\,(1-2^{n})\,B_{n}.$

It has been proved that −3 and 17 are the only prime Genocchi numbers.

Combinatorial interpretations

The exponential generating function for the signed even Genocchi numbers (−1)ⁿG_2n is

$t\tan({\frac {t}{2}})=\sum _{{n\geq 1}}(-1)^{n}G_{{2n}}{\frac {t^{{2n}}}{(2n)!}}$

They enumerate the following objects:

Permutations in S_2n−1 with descents after the even numbers and ascents after the odd numbers.

Permutations π in S_2n−2 with 1 ≤ π(2i−1) ≤ 2n−2i and 2n−2i ≤ π(2i) ≤ 2n−2.

Pairs (a₁,…,a_n−1) and (b₁,…,b_n−1) such that a_i and b_i are between 1 and i and every k between 1 and n−1 occurs at least once among the a_i's and b_i's.

Reverse alternating permutations a₁ < a₂ > a₃ < a₄ >…>a_2n−1 of [2n−1] whose inversion table has only even entries.

See also

Euler number

References

Weisstein, Eric W., "Genocchi Number", MathWorld.

Richard P. Stanley (1999). Enumerative Combinatorics, Volume 2, Exercise 5.8. Cambridge University Press. ISBN 0-521-56069-1

Gérard Viennot, Inteprétations combinatoires des nombres d'Euler et de Genocchi, Seminaire de Théorie des Nombres de Bordeaux, Volume 11 (1981-1982)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.