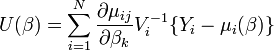Generalized estimating equation

In statistics, a generalized estimating equation (GEE) is used to estimate the parameters of a generalized linear model with a possible unknown correlation between outcomes. ^{[1] [2]}

Parameter estimates from the GEE are consistent even when the covariance structure is misspecified, under mild regularity conditions. The focus of the GEE is on estimating the average response over the population ("population-averaged" effects) rather than the regression parameters that would enable prediction of the effect of changing one or more covariates on a given individual. GEEs are usually used in conjunction with Huber-White standard error estimates, also known as "robust standard error" or "sandwich variance" estimates. In the case of a linear model with a working independence variance structure, these are known as "heteroskedasticity consistent standard error" estimators. Indeed, the GEE unified several independent formulations of these standard error estimators in a general framework.

GEEs belong to a class of semiparametric regression techniques because they rely on specification of only the first two moments. Under correct model specification and mild regularity conditions, parameter estimates from GEEs are consistent. They are a popular alternative to the likelihood–based generalized linear mixed model which is more sensitive to variance structure specification.^{[citation needed]} They are commonly used in large epidemiological studies, especially multi-site cohort studies because they can handle many types of unmeasured dependence between outcomes.

Formulation

Given a mean model, , and variance structure, , the estimating equation is formed via:^[3]

The parameter estimates solve U(β)=0 and are typically obtained via the Newton-Raphson algorithm. The variance structure is chosen to improve the efficiency of the parameter estimates. The Hessian of the solution to the GEEs in the parameter space can be used to calculate robust standard error estimates. The term "variance structure" refers to the algebraic form of the covariance matrix between outcomes, Y, in the sample. Examples of variance structure specifications include independence, exchangeable, autoregressive, stationary m-dependent, and unstructured. The most popular form of inference on GEE regression parameters is the Wald test using naive or robust standard errors, though the Score test is also valid and preferable when it is difficult to obtain estimates of information under the alternative hypothesis. The likelihood ratio test is not valid in this setting because the estimating equations are not necessarily likelihood equations. Model selection can be performed with the GEE equivalent of the Akaike Information Criterion (AIC) the Quasi-AIC (QIC).

Computation

Software for solving generalized estimating equations is available in MATLAB,^[4] SAS (proc genmod^[5]), SPSS (the gee procedure^[6]), Stata (the xtgee command^[7]) and R (packages gee^[8] and geepack^[9]).

References