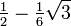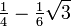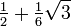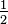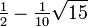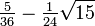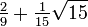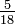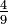Gauss–Legendre method

From Wikipedia, the free encyclopedia

In numerical analysis and scientific computing, the Gauss–Legendre methods are a family of numerical methods for ordinary differential equations. Gauss–Legendre methods are implicit Runge–Kutta methods. More specifically, they are collocation methods based on the points of Gauss–Legendre quadrature. The Gauss–Legendre method based on s points has order 2s.[1]

All Gauss–Legendre methods are A-stable.[2]

The Gauss–Legendre method of order two is the implicit midpoint rule. Its Butcher tableau is:

1/2 1/2
1

The Gauss–Legendre method of order four has Butcher tableau:

{\tfrac 12}-{\tfrac 16}{\sqrt 3} {\tfrac 14} {\tfrac 14}-{\tfrac 16}{\sqrt 3}
{\tfrac 12}+{\tfrac 16}{\sqrt 3} {\tfrac 14}+{\tfrac 16}{\sqrt 3} {\tfrac 14}
{\tfrac 12} {\tfrac 12}

The Gauss–Legendre method of order six has Butcher tableau:

{\tfrac 12}-{\tfrac 1{10}}{\sqrt {15}} {\tfrac 5{36}} {\tfrac 29}-{\tfrac 1{15}}{\sqrt {15}} {\tfrac 5{36}}-{\tfrac 1{30}}{\sqrt {15}}
{\tfrac 12} {\tfrac 5{36}}+{\tfrac 1{24}}{\sqrt {15}} {\tfrac 29} {\tfrac 5{36}}-{\tfrac 1{24}}{\sqrt {15}}
{\tfrac 12}+{\tfrac 1{10}}{\sqrt {15}} {\tfrac 5{36}}+{\tfrac 1{30}}{\sqrt {15}} {\tfrac 29}+{\tfrac 1{15}}{\sqrt {15}} {\tfrac 5{36}}
{\tfrac 5{18}} {\tfrac 49} {\tfrac 5{18}}

The computational cost of higher-order Gauss–Legendre methods is usually too high, and thus, they are rarely used.[3]

Notes

  1. ↑ Iserles 1996, p. 47
  2. ↑ Iserles 1996, p. 63
  3. ↑ Iserles 1996, p. 47

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.