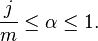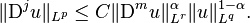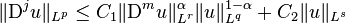Gagliardo–Nirenberg interpolation inequality

From Wikipedia, the free encyclopedia

In mathematics, the Gagliardo–Nirenberg interpolation inequality is a result in the theory of Sobolev spaces that estimates the weak derivatives of a function. The estimates are in terms of L^p norms of the function and its derivatives, and the inequality “interpolates” among various values of p and orders of differentiation, hence the name. The result is of particular importance in the theory of elliptic partial differential equations.

Statement of the inequality

The inequality concerns functions u: Rⁿ → R. Fix 1 ≤q, r ≤ ∞ and a natural number m. Suppose also that a real number α and a natural number j are such that

${\frac {1}{p}}={\frac {j}{n}}+\left({\frac {1}{r}}-{\frac {m}{n}}\right)\alpha +{\frac {1-\alpha }{q}}$

and

${\frac {j}{m}}\leq \alpha \leq 1.$

Then

every function u: Rⁿ → R that lies in L^q(Rⁿ) with m^th derivative in L^r(Rⁿ) also has j^th derivative in L^p(Rⁿ);
and, furthermore, there exists a constant C depending only on m, n, j, q, r and α such that

$\|{\mathrm {D}}^{{j}}u\|_{{L^{{p}}}}\leq C\|{\mathrm {D}}^{{m}}u\|_{{L^{{r}}}}^{{\alpha }}\|u\|_{{L^{{q}}}}^{{1-\alpha }}.$

The result has two exceptional cases:

If j = 0, mr < n and q = ∞, then it is necessary to make the additional assumption that either u tends to zero at infinity or that u lies in L^s for some finite s > 0.
If 1 < r < ∞ and m − j − n ⁄ r is a non-negative integer, then it is necessary to assume also that α ≠ 1.

For functions u: Ω → R defined on a bounded Lipschitz domain Ω ⊆ Rⁿ, the interpolation inequality has the same hypotheses as above and reads

$\|{\mathrm {D}}^{{j}}u\|_{{L^{{p}}}}\leq C_{{1}}\|{\mathrm {D}}^{{m}}u\|_{{L^{{r}}}}^{{\alpha }}\|u\|_{{L^{{q}}}}^{{1-\alpha }}+C_{{2}}\|u\|_{{L^{{s}}}}$

where s > 0 is arbitrary; naturally, the constants C₁ and C₂ depend upon the domain Ω as well as m, n etc.

Consequences

When α = 1, the L^q norm of u vanishes from the inequality, and the Gagliardo–Nirenberg interpolation inequality then implies the Sobolev embedding theorem. (Note, in particular, that r is permitted to be 1.)
Another special case of the Gagliardo–Nirenberg interpolation inequality is Ladyzhenskaya's inequality, in which m = 1, j = 0, n = 2 or 3, q and r are both 2, and p = 4.

References

Nirenberg, L. (1959). "On elliptic partial differential equations". Ann. Scuola Norm. Sup. Pisa (3) 13: 115–162.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.