Function and Concept

From Wikipedia, the free encyclopedia

"On Function and Concept" (German: Über Funktion und Begriff) is an article by Gottlob Frege, published in 1891. The article involves a clarification of his earlier distinction between concepts and objects.

In general, a concept is a function whose value is always a truth value (139). A relation is a two place function whose value is always a truth value (146).

Frege draws an important distinction between concepts on the basis of their level. Frege tells us that a first-level concept is a one-place function that correlates objects with truth-values (147). First level concepts have the value of true or false depending on whether the object falls under the concept. So, the concept $F$ has the value the True with the argument the object named by 'Jamie' if and only if Jamie falls under the concept $F$ (or is in the extension of F).

Second order concepts correlate concepts and relations with truth values. So, if we take the relation of identity to be the argument $f$ , the concept expressed by the sentence:

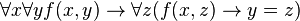
$\forall x\forall yf(x,y)\rightarrow \forall z(f(x,z)\rightarrow y=z)$

correlates the relation of identity with the True.

The conceptual range (Begriffsumfang) follows the truth value of the function:

x2 = 1 and (x + 1)2 = 2(x + 1) have the same conceptual range.

Works cited

In English: "On Function and Concept" in The Frege Reader, ed. Michael Beaney 1997, pp. 130–148

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.