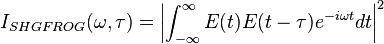Frequency-resolved optical gating
Frequency-resolved optical gating (FROG) is a general method for measuring ultrashort laser pulses, which range from subfemtosecond to about a nanosecond in length. Invented in 1991 by Rick Trebino and Daniel J. Kane, FROG was the first technique to solve this problem, which is difficult because, ordinarily, to measure an event in time, a shorter event is required with which to measure it. For example, to measure a soap bubble popping requires a strobe light with a shorter duration to freeze the action. Because ultrashort laser pulses are the shortest events ever created, before FROG, it was thought by many that their complete measurement in time was not possible. FROG, however, solved the problem by measuring an "auto-spectrogram" of the pulse, in which the pulse gates itself in a nonlinear-optical medium and the resulting gated piece of the pulse is then spectrally resolved as a function of the delay between the two pulses. Retrieval of the pulse from its FROG trace is accomplished by using a two-dimensional phase-retrieval algorithm.
FROG is currently the standard technique for measuring ultrashort laser pulses, replacing an older method called autocorrelation, which only gave a rough estimate for the pulse length. FROG is simply a spectrally resolved autocorrelation, which allows the use of a phase-retrieval algorithm to retrieve the precise pulse intensity and phase vs. time. It can measure both very simple and very complex ultrashort laser pulses, and it has measured the most complex pulse ever measured without the use of a reference pulse. Simple versions of FROG exist (with the acronym, GRENOUILLE, the French word for FROG), utilizing only a few easily aligned optical components. Both FROG and GRENOUILLE are in common use in research and industrial labs around the world.
Basics - Theory

FROG and autocorrelation share the idea of combining a pulse with itself in a nonlinear medium. Since a nonlinear medium will only produce the desired signal when both pulses are present at the same time (i.e. “Optical Gating”), varying the delay between the pulse copies and measuring the signal at each delay gives a vague estimate of the pulse length. Autocorrelators measure a pulse by measuring the intensity of the nonlinear signal field. Estimating the pulse length requires assuming a pulse shape, and the phase of the pulse electric field cannot be measured at all. FROG extends this idea by measuring the spectrum of the signal at each delay (hence “Frequency Resolved”), instead of just the intensity. This measurement creates a spectrogram of the pulse, which can be used to determine the complex electric field as a function of time or frequency as long as the nonlinearity of the medium is known.
The FROG spectrogram (usually called a FROG trace) is a graph of intensity as a function of frequency 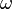 and delay
and delay  . The signal field from the nonlinear interaction is easier to express in the time domain, however, so the typical expression for the FROG trace includes a Fourier transform.
. The signal field from the nonlinear interaction is easier to express in the time domain, however, so the typical expression for the FROG trace includes a Fourier transform.
The nonlinear signal field  depends on the original pulse,
depends on the original pulse,  , and the nonlinear process used, which can almost always be expressed as
, and the nonlinear process used, which can almost always be expressed as 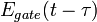 , such that
, such that 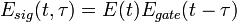 . The most common nonlinearity is second harmonic generation, where
. The most common nonlinearity is second harmonic generation, where 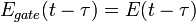 . The expression for the trace in terms of the pulse field is then:
. The expression for the trace in terms of the pulse field is then:
There are many possible variations on this basic setup. If a well-known reference pulse is available, then it may be used as a gating pulse instead of a copy of the unknown pulse. This is referred to as cross-correlation FROG or XFROG. In addition, other non-linear effects besides second harmonic generation may be used, such as third harmonic generation (THG) or polarization gating (PG). These changes will affect the expression for 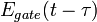 .
.
Basics - Experiment
In a typical multi-shot FROG setup, the unknown pulse is split into two copies with a beamsplitter. One copy is delayed by a known amount relative to the other. Both pulses are focused to the same point in a nonlinear medium, and the spectrum of the nonlinear signal is measured with a spectrometer. This process is repeated for many delay points.
A FROG measurement can be performed on a single shot with some minor adjustments. The two pulse copies are crossed at an angle and focused to a line instead of a point. This creates a varying delay between the two pulses along the line focus. In this configuration, it is common to use a home-made spectrometer, consisting of a diffraction grating and a camera, to capture the measurement.
Retrieval Algorithm - Generalized Projections
Although it is theoretically somewhat complex, the method of Generalized Projections has proven to be an extremely reliable method for retrieving pulses from FROG traces. Unfortunately, its sophistication is the source of some misunderstanding and mistrust from scientists in the optics community. Hence, this section will attempt to give some insight into the basic philosophy and implementation of the method, if not its detailed workings.
First, imagine a space that contains all possible signal electric fields. For a given measurement, there is a set of these fields that will satisfy the measured FROG trace. We refer to these fields as satisfying the data constraint. There is another set that consists of the signal fields that can be expressed using the form for the nonlinear interaction used in the measurement. For SHG, this is the set of fields that can be expressed in the form 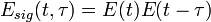 . This is referred to as satisfying the mathematical form constraint.
. This is referred to as satisfying the mathematical form constraint.
These two sets intersect at exactly one point. There is only one possible signal field that both has the correct intensity to match the data trace and fits the mathematical form dictated by the nonlinear interaction. To find that point, which will give the pulse we’re trying to measure, Generalized Projections is used. The Generalized Projections Algorithm operates in this electric field space. At each step, we find the closest point to the current guess point that will satisfy the constraint for the other set. That is, the current guess is “projected” onto the other set. This closest point becomes the new current guess, and the closest point on the first set is found. By alternating between projecting onto the mathematical constraint set and projecting onto the data constraint set, we eventually end up at the solution.
Projecting onto the data constraint set is simple. To be in that set, the magnitude squared of the signal field has to match the intensity measured by the trace. The signal field  is Fourier transformed to
is Fourier transformed to  . The closest point in the data constraint set is found by replacing the magnitude of
. The closest point in the data constraint set is found by replacing the magnitude of  by the magnitude of the data, leaving the phase of
by the magnitude of the data, leaving the phase of  intact.
intact.
Projecting onto the mathematical constraint set is not simple. Unlike the data constraint, there is not an easy way to tell which point in the mathematical constraint set is closest. A general expression for the distance between the current point and any point in the mathematical constraint set is created, and then that expression is minimized by taking the gradient of that distance with respect the current field guess. This process is discussed in more detail in this paper.
This cycle is repeated until the error between the signal guess and the data constraint (after applying the mathematical constraint) reaches some target minimum value.  can be found by simply integrating
can be found by simply integrating  with respect to delay
with respect to delay  . A second FROG trace is usually constructed mathematically from the solution and compared with the original measurement.
. A second FROG trace is usually constructed mathematically from the solution and compared with the original measurement.
Measurement Confirmation
One important feature of a FROG measurement is that many more data points are collected than are strictly necessary to find the pulse electric field. For example, say that the measured trace consists of 128 points in the delay direction and 128 points in the frequency direction. There are 128x128 total points in the trace. Using these points, an electric field is retrieved that has 2x128 points (128 for magnitude and another 128 for the phase). This is a massively overdetermined system, meaning that the number of equations is much larger than the number of unknowns. Thus the importance of each individual data point being absolutely correct is greatly reduced. This is very helpful for real world measurements that can be affected by detector noise and systematic error. Noise is extremely unlikely to affect the measured trace in a way that could be confused with a physical phenomenon in the pulse. The FROG algorithm tends to “see through” these effects due to the amount of extra information available and the use of a mathematical form constraint in finding a solution. This means that the error between an experimental FROG trace and a retrieved FROG trace is rarely zero, although it should be quite small for traces without systematic error.
Consequently, significant differences between measured and retrieved FROG traces should be investigated. The experimental setup may be misaligned, or there may be significant spatio-temporal distortions in the pulse. If the measurement averages over several or many pulses, then those pulses may vary significantly from each other.
See also
FROG techniques
- Grating-eliminated no-nonsense observation of ultrafast incident laser light e-fields (GRENOUILLE), a simplified version of FROG
- Double-Blind FROG, for measuring two pulses simultaneously
Competing techniques
- Spectral phase interferometry for direct electric-field reconstruction (SPIDER)
- Multiphoton intrapulse interference phase scan (MIIPS), a method to characterize and manipulate the ultrashort pulse.
- Frequency-resolved electro-absorption gating (FREAG)
References
- Rick Trebino (2002). Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses. Springer. ISBN 1-4020-7066-7.
- R. Trebino, K. W. DeLong, D. N. Fittinghoff, J. N. Sweetser, M. A. Krumbügel, and D. J. Kane, "Measuring Ultrashort Laser Pulses in the Time-Frequency Domain Using Frequency-Resolved Optical Gating," Review of Scientific Instruments 68, 3277-3295 (1997).
External links
- FROG Page by Rick Trebino (co-inventor of FROG)
![I_{{FROG}}(\omega ,\tau )=\left|E_{{sig}}(\omega ,\tau )\right|^{2}=\left|FT[E_{{sig}}(t,\tau )]\right|^{2}=\left|\int _{{-\infty }}^{{\infty }}E_{{sig}}(t,\tau )e^{{-i\omega t}}dt\right|^{2}](/2014-wikipedia_en_all_02_2014/I/media/8/9/a/e/89ae41e289686acd27c3a5f03f9a1f40.png)