Fragility

Arrhenius plot of fragility of glass formation, including strong and fragile glass formers. This representation of fragility is known as an "Angell Plot".

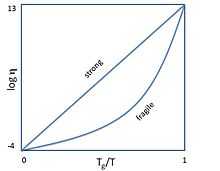
In glass physics, fragility characterizes how rapidly the dynamics of a material slow down as it is cooled toward the glass transition: materials with a higher fragility have a relatively narrow glass transition temperature range, while those with low fragility have a relatively broad glass transition temperature range. Physically, fragility may be related to the presence of dynamical heterogeneity in glasses, as well as to the breakdown of the usual Stokes-Einstein relationship between viscosity and diffusion.

Definition

Formally, fragility reflects to what degree the temperature dependence of the viscosity (or relaxation time) deviates from Arrhenius behavior.^[1] This classification was originally proposed by Austen Angell.^[1][2] The most common definition of fragility characterizes the slope of the viscosity (or relaxation time) of a material with temperature as it approaches the glass transition temperature from above:

where is viscosity, is the glass transition temperature, m is fragility, and T is temperature.^[3] Glass-formers with a high fragility are called "fragile"; those with a low fragility are called "strong".^[4] For example, silica has a relatively low fragility and is called "strong", whereas some polymers have relatively high fragility^[3] and are called "fragile". Fragility has no direct relationship with the colloquial meaning of the word "fragility", which more closely relates to the brittleness of a material.

Several fragility parameters have been introduced to characterise the fragility of liquids, e.g. Bruning-Sutton,^[5] Avramov ^[6] and Doremus fragility parameters.^[7] The Bruning-Sutton fragility parameter m relies on the curvature or slope of the viscosity curves. The Avramov fragility parameter α is based on a Kohlraush-type formula of viscosity derived for glasses: strong liquids have α ≈ 1 whereas liquids with higher α values become more fragile. Doremus indicated that practically all melts deviate from the Arrhenius behaviour, e.g. the activation energy of viscosity changes from a high Q_H at low temperature to a low Q_L at high temperature. However asymptotically both at low and high temperatures the activation energy of viscosity becomes constant, e.g. independent of temperature. Changes that occur in the activation energy are unambiguously characterised by the ratio between the two values of activation energy at low and high temperatures, which Doremus suggested could be used as a fragility criterion: R_D=Q_H/Q_L. The higher is R_D the more fragile are the liquids, Doremus’ fragility ratios range from 1.33 for germania to 7.26 for diopside melts.

The Doremus’ criterion of fragility can be expressed in terms of thermodynamic parameters of the defects mediating viscous flow in the oxide melts: R_D=1+H_d/H_m, where H_d is the enthalpy of formation and H_m is the enthalpy of motion of such defects. Hence the fragility of oxide melts is an intrinsic thermodynamic parameter of melts which can be determined unambiguously by experiment.^[8]

Recent synchrotron - radiation X-ray diffraction experiments showed a clear link between structure evolution of the supercooled liquid on cooling, for example, intensification of Ni-P and Cu-P peaks in the radial distribution function close to the glass-transition, and liquid fragility.^[9][10][11]

Physical Implications

The physical origin of the non-Arrhenius behavior of fragile glass formers is an area of active investigation in glass physics. Advances over the last decade have linked this phenomenon with the presence of locally heterogeneous dynamics in fragile glass formers; i.e. the presence of distinct (if transient) slow and fast regions within the material.^[1][12] This effect also been connected to the breakdown of the Einstein-Stokes relationship between diffusion and viscosity in fragile liquids.^[12]

References