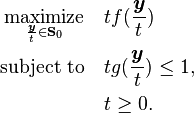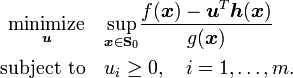Fractional programming

From Wikipedia, the free encyclopedia

In mathematical optimization, fractional programming is a generalization of linear-fractional programming. The objective function in a fractional program is a ratio of two functions that are in general nonlinear. The ratio to be optimized often describes some kind of efficiency of a system.

Definition

Let 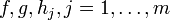$f,g,h_{j},j=1,\ldots ,m$ be real-valued functions defined on a set 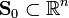${\mathbf {S}}_{0}\subset {\mathbb {R}}^{n}$ . Let ${\mathbf {S}}=\{{\boldsymbol {x}}\in {\mathbf {S}}_{0}:h_{j}({\boldsymbol {x}})\leq 0,j=1,\ldots ,m\}$ . The nonlinear program

${\underset {{\boldsymbol {x}}\in {\mathbf {S}}}{{\text{maximize}}}}\quad {\frac {f({\boldsymbol {x}})}{g({\boldsymbol {x}})}},$

where $g({\boldsymbol {x}})>0$ on ${\mathbf {S}}$ , is called a fractional program.

Concave fractional programs

A fractional program in which f is nonnegative and concave, g is positive and convex, and S is a convex set is called a concave fractional program. If g is affine, f does not have to be restricted in sign. The linear fractional program is a special case of a concave fractional program where all functions 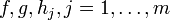$f,g,h_{j},j=1,\ldots ,m$ are affine.

Properties

The function 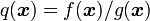$q({\boldsymbol {x}})=f({\boldsymbol {x}})/g({\boldsymbol {x}})$ is semistrictly quasiconcave on S. If f and g are differentiable, then q is pseudoconcave. In a linear fractional program, the objective function is pseudolinear.

Transformation to a concave program

By the transformation ${\boldsymbol {y}}={\frac {{\boldsymbol {x}}}{g({\boldsymbol {x}})}};t={\frac {1}{g({\boldsymbol {x}})}}$ , any concave fractional program can be transformed to the equivalent parameter-free concave program ^[1]

${\begin{aligned}{\underset {{\frac {{\boldsymbol {y}}}{t}}\in {\mathbf {S}}_{0}}{{\text{maximize}}}}\quad &tf({\frac {{\boldsymbol {y}}}{t}})\\{\text{subject to}}\quad &tg({\frac {{\boldsymbol {y}}}{t}})\leq 1,\\&t\geq 0.\end{aligned}}$

If g is affine, the first constraint is changed to 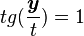$tg({\frac {{\boldsymbol {y}}}{t}})=1$ and the assumption that f is nonnegative may be dropped.

Duality

The Lagrangean dual of the equivalent concave program is

${\begin{aligned}{\underset {{\boldsymbol {u}}}{{\text{minimize}}}}\quad &{\underset {{\boldsymbol {x}}\in {\mathbf {S}}_{0}}{\operatorname {sup}}}{\frac {f({\boldsymbol {x}})-{\boldsymbol {u}}^{T}{\boldsymbol {h}}({\boldsymbol {x}})}{g({\boldsymbol {x}})}}\\{\text{subject to}}\quad &u_{i}\geq 0,\quad i=1,\dots ,m.\end{aligned}}$

Notes

↑ Schaible, Siegfried (1974). "Parameter-free Convex Equivalent and Dual Programs". Zeitschrift für Operations Research 18 (5): 187–196. doi:10.1007/BF02026600. MR 351464.

References

Avriel, Mordecai; Diewert, Walter E.; Schaible, Siegfried; Zang, Israel (1988). Generalized Concavity. Plenum Press.
Schaible, Siegfried (1983). "Fractional programming". Zeitschrift für Operations Research 27: 39–54.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.