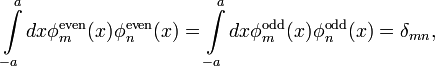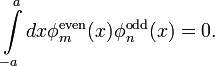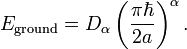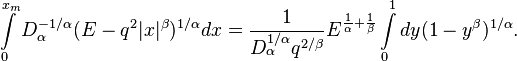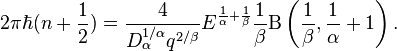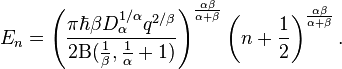Fractional Schrödinger equation
The fractional Schrödinger equation is a fundamental equation of fractional quantum mechanics. It was discovered by Nick Laskin (1999) as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by Nick Laskin.[1]
Fundamentals
The fractional Schrödinger equation in the form originally obtained by Nick Laskin is:[2]
- r is the 3-dimensional position vector,
- ħ is the reduced Planck constant,
- ψ(r, t) is the wavefunction, which is the quantum mechanical probability amplitude for the particle to have a given position r at any given time t,
- V(r, t) is a potential energy,
- Δ = ∂2/∂r2 is the Laplace operator.
Further,
- Dα is a scale constant with physical dimension [Dα] = [energy]1 − α·[length]α[time]−α, at α = 2, D2 =1/2m, where m is a particle mass,
- the operator (−ħ2Δ)α/2 is the 3-dimensional fractional quantum Riesz derivative defined by (see, Ref.[2]);
Here, the wave functions in the position and momentum spaces;  and
and 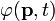 are related each other by the 3-dimensional Fourier transforms:
are related each other by the 3-dimensional Fourier transforms:
The index α in the fractional Schrödinger equation is the Lévy index, 1 < α ≤ 2. Thus, the fractional Schrödinger equation includes a space derivative of fractional order α instead of the second order (α = 2) space derivative in the standard Schrödinger equation. Thus, the fractional Schrödinger equation is a fractional differential equation in accordance with modern terminology.[3] This is the main point of the term fractional Schrödinger equation or a more general term fractional quantum mechanics.[4] At α = 2 fractional Schrödinger equation becomes the well-known Schrödinger equation.
The fractional Schrödinger equation has the following operator form
where the fractional Hamilton operator  is given by
is given by
The Hamilton operator,  corresponds to the classical mechanics Hamiltonian function
corresponds to the classical mechanics Hamiltonian function
where p and r are the momentum and the position vectors respectively.
Time-independent fractional Schrödinger equation
The special case when the Hamiltonian  is independent of time
is independent of time
is of great importance for physical applications. It is easy to see that in this case there exist the special solution of the fractional Schrödinger equation
where 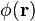 satisfies
satisfies
or
This is the time-independent fractional Schrödinger equation.
Thus, we see that the wave function  oscillates with a definite frequency. In classical physics the frequency corresponds to the energy. Therefore, the quantum mechanical state has a definite energy E.
The probability to find a particle at
oscillates with a definite frequency. In classical physics the frequency corresponds to the energy. Therefore, the quantum mechanical state has a definite energy E.
The probability to find a particle at  is the absolute square of the wave function
is the absolute square of the wave function 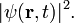 Because of time-independent fractional Schrödinger equation this is equal to
Because of time-independent fractional Schrödinger equation this is equal to  and does not depend upon the time.
That is, the probability of finding the particle at
and does not depend upon the time.
That is, the probability of finding the particle at  is independent of the time. One can say that the system is in a stationary
state. In other words, there is no variation in the probabilities as a function of time.
is independent of the time. One can say that the system is in a stationary
state. In other words, there is no variation in the probabilities as a function of time.
Probability current density
The continuity equation for probability current and density follows from the fractional Schrödinger equation:
where  is the quantum mechanical probability density and the vector
is the quantum mechanical probability density and the vector  can be called by the fractional probability current density vector
can be called by the fractional probability current density vector
where we use the notation (see also matrix calculus):  .
.
Introducing the momentum operator  we can write the vector
we can write the vector  in the form (see, Ref.[2])
in the form (see, Ref.[2])
This is fractional generalization of the well-known equation for probability current density vector of standard quantum mechanics (see, Ref.[7]).
Velocity operator
The quantum mechanical velocity operator  is defined as follows:
is defined as follows:
Straightforward calculation results in (see, Ref.[2])
Hence,
To get the probability current density equal to 1 (the current when one particle passes through unit area per unit time) the wave function of a free particle has to be normalized as
where  is the particle velocity,
is the particle velocity,  .
.
Then we have
that is, the vector  is indeed the unit vector.
is indeed the unit vector.
Physical applications
Fractional Bohr atom
When  is the potential energy of hydrogenlike atom,
is the potential energy of hydrogenlike atom,
where e is the electron charge and Z is the atomic number of the hydrogenlike atom, (so Ze is the nuclear charge of the atom), we come to following fractional eigenvalue problem,
This eigenvalue problem has first been solved in.[5]
Using the first Niels Bohr postulate yields
and it gives us the equation for the Bohr radius of the fractional hydrogenlike atom
Here a0 is the fractional Bohr radius (the radius of the lowest, n = 1, Bohr orbit) defined as,
The energy levels of the fractional hydrogenlike atom are given by
where E0 is the binding energy of the electron in the lowest Bohr orbit that is, the energy required to put it in a state with E = 0 corresponding to n = ∞,
The energy (α − 1)E0 divided by ħc, (α − 1)E0/ħc, can be considered as fractional generalization of the
Rydberg constant of standard quantum mechanics. For α = 2 and Z = 1 the formula
 is transformed into
is transformed into
-
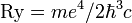 ,
,
which is the well-known expression for the Rydberg formula.
According to the second Niels Bohr postulate, the frequency of radiation 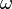 associated with the transition, say, for example from the orbit m to the orbit n, is,
associated with the transition, say, for example from the orbit m to the orbit n, is,
-
![\omega ={\frac {(1-\alpha )E_{{0}}}{\hbar }}\left[{\frac {1}{n^{{{\frac {\alpha }{\alpha -1}}}}}}-{\frac {1}{m^{{{\frac {\alpha }{\alpha -1}}}}}}\right]](/2014-wikipedia_en_all_02_2014/I/media/c/f/0/4/cf04d56f6d5313f9fceb257c5866d79d.png) .
.
The above equations are fractional generalization of the Bohr model. In the special Gaussian case, when (α = 2) those equations give us the well-known results of the Bohr model.[6]
The infinite potential well
A particle in a one-dimensional well moves in a potential field  , which is zero for
, which is zero for
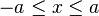 and which is infinite elsewhere,
and which is infinite elsewhere,
It is evident a priori that the energy spectrum will be discrete. The solution of the fractional Schrödinger equation for the stationary state with well-defined energy E is described by a wave function 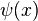 , which can be written as
, which can be written as
 ,
,
where 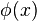 , is now time independent.
In regions (i) and (iii),
the fractional Schrödinger
equation can be satisfied only if we take
, is now time independent.
In regions (i) and (iii),
the fractional Schrödinger
equation can be satisfied only if we take  . In the middle region
(ii), the time-independent fractional Schrödinger equation is
. In the middle region
(ii), the time-independent fractional Schrödinger equation is
This equation defines the wave functions and the energy spectrum within region (ii), while outside
of the region (ii), x<-a and x>a, the wave functions are zero. The wave function 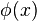 has to be continuous everywhere, thus we impose the boundary conditions
has to be continuous everywhere, thus we impose the boundary conditions 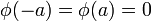 for the solutions of the time-independent fractional Schrödinger equation (see, Ref.[5]). Then the solution in region (ii) can be written as
for the solutions of the time-independent fractional Schrödinger equation (see, Ref.[5]). Then the solution in region (ii) can be written as
where k is given by
The even (under reflection  ) solution
) solution 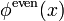 satisfies the boundary conditions if
satisfies the boundary conditions if
The odd (under reflection  ) solution
) solution  satisfies the boundary conditions if
satisfies the boundary conditions if
It is easy to check that the normalized solutions are
and
Solutions 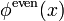 and
and  have the
property that
have the
property that
where 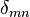 is the Kronecker symbol and
is the Kronecker symbol and
The eigenvalues of the particle in an infinite potential well are (see, Ref.[5])
It is obvious that in the Gaussian case (α = 2) above equations are transformed into the standard quantum mechanical equations for a particle in a box (for example, see Eq.(20.7) in [7])
The state of the lowest energy, the ground state, in the infinite potential
well is represented by the  at n=1,
at n=1,
and its energy is
Fractional quantum oscillator
Fractional quantum oscillator introduced by Nick Laskin (see, Ref.[2]) is the fractional quantum mechanical model with the Hamiltonian operator 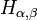 defined as
defined as
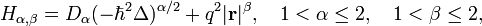 ,
,
where q is interaction constant.
The fractional Schrödinger equation for the wave
function  of the fractional quantum oscillator is,
of the fractional quantum oscillator is,
Aiming to search for solution in form
we come to the time-independent fractional Schrödinger equation,
The Hamiltonian 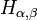 is the fractional
generalization of the 3D quantum harmonic oscillator Hamiltonian of standard quantum
mechanics.
is the fractional
generalization of the 3D quantum harmonic oscillator Hamiltonian of standard quantum
mechanics.
Energy levels of the 1D fractional quantum oscillator in semiclassical approximation
The energy levels of 1D fractional quantum oscillator with the Hamiltonian function  can be found in semiclassical approximation.
can be found in semiclassical approximation.
We set the total energy equal to E, so that
whence
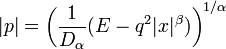 .
.
At the turning points 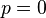 . Hence, the classical motion is
possible in the range
. Hence, the classical motion is
possible in the range 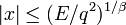 .
.
A routine use of the Bohr-Sommerfeld quantization rule yields
where the notation  means the integral over one complete period of
the classical motion and
means the integral over one complete period of
the classical motion and 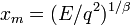 is the turning point
of classical motion.
is the turning point
of classical motion.
To evaluate the integral in the right hand we introduce a new variable 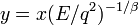 . Then we have
. Then we have
The integral over dy can be expressed in terms of the Beta-function,
Therefore
The above equation gives the energy levels of stationary states for the 1D fractional quantum oscillator (see, Ref.[2]),
This equation is generalization of the well-known energy levels equation of the
standard quantum harmonic oscillator (see, Ref.[7]) and
is transformed into it at α = 2 and β = 2.
It follows from this equation that at  the energy levels are equidistant. When
the energy levels are equidistant. When 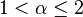 and
and  the equidistant energy levels can be for α = 2 and β = 2 only. It means that the only standard quantum
harmonic oscillator has an equidistant energy spectrum.
the equidistant energy levels can be for α = 2 and β = 2 only. It means that the only standard quantum
harmonic oscillator has an equidistant energy spectrum.
See also
- Schrödinger equation
- Path integral formulation
- Relation between Schrödinger's equation and the path integral formulation of quantum mechanics
- Fractional calculus
- Quantum harmonic oscillator
References
- ↑ N. Laskin, (2000), Fractional Quantum Mechanics and Lévy Path Integrals. Physics Letters 268A, 298-304.
- ↑ N. Laskin, (2002), Fractional Schrödinger equation, Physical Review E66, 056108 7 pages. (also available online: http://arxiv.org/abs/quant-ph/0206098)
- ↑ S. G. Samko, A. A. Kilbas, and O. I. Marichev, Fractional Integrals and Derivatives, Theory and Applications ~Gordon and Breach, Amsterdam, 1993
- ↑ N. Laskin, (2000), Fractional Quantum Mechanics, Physical Review E62, 3135-3145. (also available online: http://arxiv.org/abs/0811.1769)
- ↑ N. Laskin, (2000), Fractals and quantum mechanics. Chaos 10, 780-790
- ↑ N. Bohr, (1913), Phil. Mag. 26, 1, 476, 857
- ↑ L.D. Landau and E.M. Lifshitz, Quantum mechanics (Non-relativistic Theory), Vol.3, Third Edition, Course of Theoretical Physics, Butterworth-Heinemann, Oxford, 2003
- Richard Herrmann (2011). "9". Fractional Calculus, An Introduction for Physicists. World Scientific. ISBN 981 4340 24 3.
- J. Klafter, S.C. Lim, R. Metzler (2012). Fractional Dynamics: Recent Advances. World Scientific. p. 426. ISBN 981-434-059-6.
- J.S. Moreno (2008). Progress in Statistical Mechanics Research. Nova Publishers. p. 10. ISBN 160-456-028-2.
- L. Debnath (2005). Nonlinear partial differential equations for scientists and engineers (2nd ed.). Springer. pp. 126–127. ISBN 0-817-643-230.
- T. Myint U., L. Debnath (2007). Linear partial differential equations for scientists and engineers (4th ed.). Springer. p. 520. ISBN 0-817-645-608.
- Issues in Applied Mathematics. Scholarly Editions. 2012. ISBN 146-496-507-2.
- V.E. Tarasov (2010). "19". Fractional dynamics. Nonlinear physical science 0. Springer. ISBN 3-642-140-033.
- J. Sabatier, O.P.Agrawal, J.A.T.Machado (2007). Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering. Springer. ISBN 1-402-060-424.
- D. Baleanu, J.A.T. Machado, A.C.J. Luo (2012). "17". Fractional Dynamics and Control. Springer. ISBN 1-461-404-576.
Further reading
- Xiaoyi Guo and Mingyu Xu, Some physical applications of fractional Schrödinger equation. J. Math. Phys. 47, 082104 (2006).
- S. Wang, M. Xu, Generalized fractional Schrödinger equation with space-time fractional derivatives J. Math. Phys. 48 (2007) 043502
- Bayın, Selçuk Ş., On the consistency of the solutions of the space fractional Schrödinger equation. Journal of Mathematical Physics, Volume 53, Issue 4, pp. 042105-042105-9 (2012)
- Jianping Dong, , Mingyu Xu, Some solutions to the space fractional Schrödinger equation using momentum representation method , J. Math. Phys. 48, 072105 (2007).
- Jianping Dong, , Mingyu Xu, Space–time fractional Schrödinger equation with time-independent potentials, Journal of Mathematical Analysis and Applications Volume 344, Issue 2, Pages 1005–1017 (2008).
- A. Iomin, Fractional-time quantum dynamics. Phys. Rev. E 80, (2009) 022103.
- N. Laskin, Fractals and quantum mechanics. Chaos 10(2000) 780-790
- M. Naber, Time fractional Schrodinger equation. J. Math. Phys. 45 (2004) 3339-3352. arXiv:math-ph/0410028
- V.E. Tarasov, Fractional Heisenberg equation. Phys. Lett. A 372 (2008) 2984-2988.
- V.E. Tarasov, Weyl quantization of fractional derivatives. J. Math. Phys. 49 (2008) 102112.
- Edmundo Capelas de Oliveira, Felix Silva Costa, and Jayme Vaz, Jr., The fractional Schrödinger equation for delta potentials, J. Math. Phys. 51, 123517 (2010).
- E Capelas de Oliveira and Jayme Vaz Jr, "Tunneling in Fractional Quantum Mechanics" Journal of Physics A Volume 44 (2011) 185303.

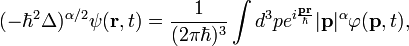
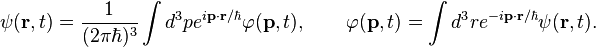

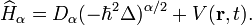
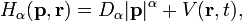
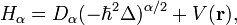
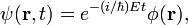
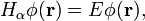
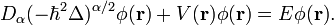
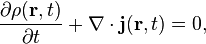
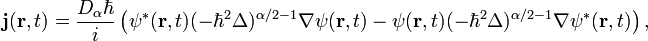
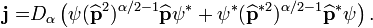
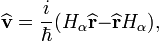


![\psi ({\mathbf {r}},t)={\sqrt {{\frac {\alpha }{2{\mathrm {v}}}}}}\exp \left[{\frac {i}{\hbar }}({\mathbf {p}}\cdot {\mathbf {r}}-Et)\right],\qquad E=D_{{\alpha }}|{\mathbf {p}}|^{{\alpha }},\qquad 1<\alpha \leq 2,](/2014-wikipedia_en_all_02_2014/I/media/c/b/8/6/cb8642ebe5b6d8f2ced41b4f00cfe857.png)









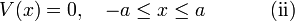

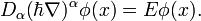
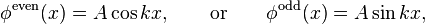

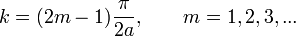

![\phi _{m}^{{{\mathrm {even}}}}(x)={\frac 1{{\sqrt {a}}}}\cos \left[(m-{\frac 12}){\frac {\pi x}a}\right],](/2014-wikipedia_en_all_02_2014/I/media/4/e/3/d/4e3d5bc5d9af973e3207c82a0bbe05b4.png)