Fractional-order control

From Wikipedia, the free encyclopedia

Fractional-order control (FOC) is a field of control theory that uses the fractional-order integrator as part of the control system design toolkit.

The fundamental advantage of FOC is that the fractional-order integrator weights history using a function that decays with a power-law tail. The effect is that the effects of all time are computed for each iteration of the control algorithm. This creates a 'distribution of time constants,' the upshot of which is there is no particular time constant, or resonance frequency, for the system.

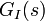In fact, the fractional integral operator {\frac {1}{s^{{\lambda }}}} is different from any integer-order rational transfer function {G_{{I}}}(s), in the sense that it is a non-local operator that possesses an infinite memory and takes into account the whole history of its input signal.[1]

Fractional-order control shows promise in many controlled environments that suffer from the classical problems of overshoot and resonance, as well as time diffuse applications such as thermal dissipation and chemical mixing.

See also

External links

References

  1. ↑ M. S. Tavazoei, M. Haeri, S. Bolouki, and M. Siami, "Stability preservation analysis for frequency-based methods in numerical simulation of fractional-order systems," SIAM Journal on Numerical Analysis, vol. 47, pp. 321–338, 2008.


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.