Fpqc morphism

From Wikipedia, the free encyclopedia

In algebraic geometry, an fpqc morphism $f:X\to Y$ of schemes is a faithfully flat morphism that satisfies the following equivalent conditions:

Every quasi-compact open subset of Y is the image of a quasi-compact open subset of X.
There exists a covering $V_{i}$ of Y by open affine subschemes such that each $V_{i}$ is the image of a quasi-compact open subset of X.
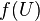Each point $x\in X$ has a neighborhood $U$ such that $f(U)$ is open and 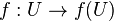$f:U\to f(U)$ is quasi-compact.
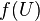Each point $x\in X$ has a quasi-compact neighborhood such that $f(U)$ is open affine.

Examples: An open faithfully flat morphism is fpqc.

An fpqc morphism satisfies the following properties:

The composite of fpqc morphisms is fpqc.
A base change of an fpqc morphism is fpqc.
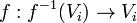If $f:X\to Y$ is a morphism of schemes and if there is an open covering $V_{i}$ of Y such that the $f:f^{{-1}}(V_{i})\to V_{i}$ is fpqc, then f is fpqc.
A faithfully flat morphism that is locally of finite presentation (i.e., fppf) is fpqc.
If $f:X\to Y$ is an fpqc morphism, a subset of Y is open in Y if and only if its inverse image under f is open in X.

See also

References

Angelo Vistoli, "Notes on Grothendieck topologies, fibered categories and descent theory." arXiv:math.AG/0412512v4

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.