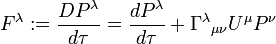Four-force

From Wikipedia, the free encyclopedia

In the special theory of relativity four-force is a four-vector that replaces the classical force; the four-force is the four-vector defined as the change in four-momentum over the particle's own time:

{\mathbf {F}}={d{\mathbf {P}} \over d\tau }.

For a particle of constant invariant mass m > 0, 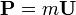{\mathbf {P}}=m{\mathbf {U}}\, where {\mathbf {U}}=\gamma (c,{\mathbf {u}})\, is the four-velocity, so we can relate the four-force with the four-acceleration as in Newton's second law:

{\mathbf {F}}=m{\mathbf {A}}=\left(\gamma {{\mathbf {f}}\cdot {\mathbf {u}} \over c},\gamma {{\mathbf f}}\right).

Here

{{\mathbf f}}={d \over dt}\left(\gamma m{{\mathbf u}}\right)={d{\mathbf {p}} \over dt}

and

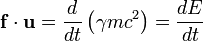{{\mathbf {f}}\cdot {\mathbf {u}}}={d \over dt}\left(\gamma mc^{2}\right)={dE \over dt}.

where {\mathbf {u}}, {\mathbf {p}} and {\mathbf {f}} are 3-vectors describing the velocity and the momentum of the particle and the force acting on it respectively.

In general relativity the relation between four-force, and four-acceleration remains the same, but the elements of the four-force are related to the elements of the four-momentum through a covariant derivative with respect to proper time.

F^{\lambda }:={\frac {DP^{\lambda }}{d\tau }}={\frac {dP^{\lambda }}{d\tau }}+\Gamma ^{\lambda }{}_{{\mu \nu }}U^{\mu }P^{\nu }

Examples

In special relativity, Lorentz 4-force (4-force acting to charged particle situated in electromagnetic field) can be expressed as:

F_{\mu }=qE_{{\mu \nu }}U^{\nu }, where E_{{\mu \nu }} - electromagnetic tensor, U^{\nu } - 4-velocity, q - electric charge.

See also

References

  • Rindler, Wolfgang (1991). Introduction to Special Relativity (2nd ed.). Oxford: Oxford University Press. ISBN 0-19-853953-3. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.