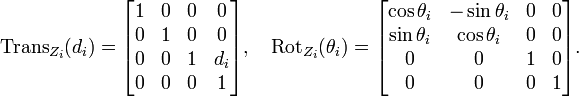Forward kinematics

From Wikipedia, the free encyclopedia

An articulated six DOF robotic arm uses forward kinematics to position the gripper.

The forward kinematics equations define the trajectory of the end-effector of a PUMA robot reaching for parts.

Forward kinematics refers to the use of the kinematic equations of a robot to compute the position of the end-effector from specified values for the joint parameters.^[1] The kinematics equations of the robot are used in robotics, computer games, and animation. The reverse process that computes the joint parameters that achieve a specified position of the end-effector is known as inverse kinematics.

Kinematics equations

The kinematics equations for the series chain of a robot are obtained using a rigid transformation [Z] to characterize the relative movement allowed at each joint and separate rigid transformation [X] to define the dimensions of each link. The result is a sequence of rigid transformations alternating joint and link transformations from the base of the chain to its end link, which is equated to the specified position for the end link,

$[T]=[Z_{1}][X_{1}][Z_{2}][X_{2}]\ldots [X_{{n-1}}][Z_{n}],\!$

where [T] is the transformation locating the end-link. These equations are called the kinematics equations of the serial chain.^[2]

Link transformations

In 1955, Jacques Denavit and Richard Hartenberg introduced a convention for the definition of the joint matrices [Z] and link matrices [X] to standardize the coordinate frame for spatial linkages.^[3]^[4] This convention positions the joint frame so that it consists of a screw displacement along the Z-axis

$[Z_{i}]=\operatorname {Trans}_{{Z_{{i}}}}(d_{i})\operatorname {Rot}_{{Z_{{i}}}}(\theta _{i}),$

and it positions the link frame so it consists of a screw displacement along the X-axis,

$[X_{i}]=\operatorname {Trans}_{{X_{i}}}(a_{{i,i+1}})\operatorname {Rot}_{{X_{i}}}(\alpha _{{i,i+1}}).$

Using this notation, each transformation-link goes along a serial chain robot, and can be described by the coordinate transformation,

${}^{{i-1}}T_{{i}}=[Z_{i}][X_{i}]=\operatorname {Trans}_{{Z_{{i}}}}(d_{i})\operatorname {Rot}_{{Z_{{i}}}}(\theta _{i})\operatorname {Trans}_{{X_{i}}}(a_{{i,i+1}})\operatorname {Rot}_{{X_{i}}}(\alpha _{{i,i+1}}),$

where θ_i, d_i, α_i,i+1 and a_i,i+1 are known as the Denavit-Hartenberg parameters.

Kinematics equations revisited

The kinematics equations of a serial chain of n links, with joint parameters θ_i are given by^[5]

$[T]={}^{{0}}T_{n}=\prod _{{i=1}}^{n}{}^{{i-1}}T_{i}(\theta _{i}),$

where ${}^{{i-1}}T_{i}(\theta _{i})$ is the transformation matrix from the frame of link $i$ to link $i-1$ . In robotics, these are conventionally described by Denavit–Hartenberg parameters.^[6]

Denavit-Hartenberg matrix

The matrices associated with these operations are:

$\operatorname {Trans}_{{Z_{{i}}}}(d_{i})={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&d_{i}\\0&0&0&1\end{bmatrix}},\quad \operatorname {Rot}_{{Z_{{i}}}}(\theta _{i})={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}&0&0\\\sin \theta _{i}&\cos \theta _{i}&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}.$

Similarly,

$\operatorname {Trans}_{{X_{i}}}(a_{{i,i+1}})={\begin{bmatrix}1&0&0&a_{{i,i+1}}\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}},\quad \operatorname {Rot}_{{X_{i}}}(\alpha _{{i,i+1}})={\begin{bmatrix}1&0&0&0\\0&\cos \alpha _{{i,i+1}}&-\sin \alpha _{{i,i+1}}&0\\0&\sin \alpha _{{i,i+1}}&\cos \alpha _{{i,i+1}}&0\\0&0&0&1\end{bmatrix}}.$

The use of the Denavit-Hartenberg convention yields the link transformation matrix, [^i-1T_i] as

$\operatorname {}^{{i-1}}T_{i}={\begin{bmatrix}\cos \theta _{i}&-\sin \theta _{i}\cos \alpha _{{i,i+1}}&\sin \theta _{i}\sin \alpha _{{i,i+1}}&a_{{i,i+1}}\cos \theta _{i}\\\sin \theta _{i}&\cos \theta _{i}\cos \alpha _{{i,i+1}}&-\cos \theta _{i}\sin \alpha _{{i,i+1}}&a_{{i,i+1}}\sin \theta _{i}\\0&\sin \alpha _{{i,i+1}}&\cos \alpha _{{i,i+1}}&d_{i}\\0&0&0&1\end{bmatrix}},$

known as the Denavit-Hartenberg matrix.

References

↑ Paul, Richard (1981). Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators. MIT Press, Cambridge, MA. ISBN 978-0-262-16082-7.
↑ J. M. McCarthy, 1990, Introduction to Theoretical Kinematics, MIT Press, Cambridge, MA.
↑ J. Denavit and R.S. Hartenberg, 1955, "A kinematic notation for lower-pair mechanisms based on matrices." Trans ASME J. Appl. Mech, 23:215–221.
↑ Hartenberg, R. S., and J. Denavit. Kinematic Synthesis of Linkages. New York: McGraw-Hill, 1964 on-line through KMODDL
↑ Jennifer Kay. "Introduction to Homogeneous Transformations & Robot Kinematics". Retrieved 2010-09-11.
↑ Learn About Robots. "Robot Forward Kinematics". Retrieved 2007-02-01.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.