Flipped SU(5)
The Flipped SU(5) model is a Grand Unified Theory (GUT) theory first contemplated by Stephen Barr in 1982,[1] and by Dimitri Nanopoulos and others in 1984.[2][3] Ignatios Antoniadis, John Ellis, John Hagelin, and Nanopoulos developed the supersymmetric flipped SU(5), derived from the deeper-level superstring.[4]
Current efforts to explain the theoretical underpinnings for observed neutrino masses are being developed in the context of supersymmetric flipped SU(5).[5]
Flipped SU(5) is not a fully unified model, because the U(1)y factor of the SM gauge group is within the U(1) factor of the GUT group. The addition of states below Mx in this model, while solving certain threshold correction issues in string theory, makes the model merely descriptive, rather than predictive.[6]
The Model
The Flipped SU(5) model states that the gauge group is:
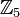
Fermions form three families, each consisting of the representations
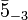 for the lepton doublet, L, and the up quarks
for the lepton doublet, L, and the up quarks 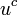 ;
; for the quark doublet,Q, the down quark,
for the quark doublet,Q, the down quark, 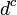 and the right-handed neutrino, N;
and the right-handed neutrino, N;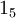 for the charged leptons,
for the charged leptons,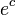 .
.
This assignment includes three right-handed neutrinos, which have never been observed, but are often postulated to explain the lightness of the observed neutrinos and neutrino oscillations. There is also a  and/or
and/or 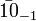 called the Higgs fields which acquire a VEV, yielding the spontaneous symmetry breaking
called the Higgs fields which acquire a VEV, yielding the spontaneous symmetry breaking
![[SU(5)\times U(1)_{\chi }]/{\mathbb {Z}}_{5}](/2014-wikipedia_en_all_02_2014/I/media/3/6/3/a/363ac1e117df516e6d14d031f10deb18.png) to
to ![[SU(3)\times SU(2)\times U(1)_{Y}]/{\mathbb {Z}}_{6}](/2014-wikipedia_en_all_02_2014/I/media/b/4/c/b/b4cb92cd3a5be3e98e02761cf022404b.png)
The SU(5) representations transform under this subgroup as the reducible representation as follows:
-
 (uc and l)
(uc and l) -
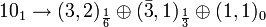 (q, dc and νc)
(q, dc and νc) -
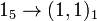 (ec)
(ec)
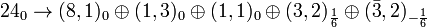 .
.
Comparison with the standard SU(5)
The name "flipped" SU(5) arose in comparison to the "standard" SU(5) model of Georgi-Glashow, in which 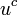 and
and 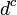 quark are respectively assigned to the 10 and 5 representation. In comparison with the standard SU(5), the flipped SU(5) can accomplish the spontaneous symmetry breaking using Higgs fields of dimension 10, while the standard SU(5) requires both a 5- and 45-dimensional Higgs.
quark are respectively assigned to the 10 and 5 representation. In comparison with the standard SU(5), the flipped SU(5) can accomplish the spontaneous symmetry breaking using Higgs fields of dimension 10, while the standard SU(5) requires both a 5- and 45-dimensional Higgs.
The sign convention for U(1)χ varies from article/book to article.
The hypercharge Y/2 is a linear combination (sum) of the  of SU(5) and χ/5.
of SU(5) and χ/5.
There are also the additional fields 5-2 and 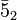 containing the electroweak Higgs doublets.
containing the electroweak Higgs doublets.
Calling the representations for example, 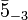 and 240 is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableaux or Dynkin diagrams with numbers on their vertices, and is a standard used by GUT
theorists.
and 240 is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableaux or Dynkin diagrams with numbers on their vertices, and is a standard used by GUT
theorists.
Since the homotopy group
this model does not predict monopoles. See Hooft-Polyakov monopole.

spacetime
The N=1 superspace extension of 3+1 Minkowski spacetime
spatial symmetry
N=1 SUSY over 3+1 Minkowski spacetime with R-symmetry
gauge symmetry group
[SU(5)× U(1)χ]/Z5
global internal symmetry
Z2 (matter parity) not related to U(1)R in any way for this particular model
vector superfields
Those associated with the SU(5)× U(1)χ gauge symmetry
chiral superfields
As complex representations:
| label | description | multiplicity | SU(5)× U(1)χ rep | 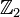 rep rep | U(1)R |
| 10H | GUT Higgs field | 1 | 101 | + | 0 |
 | GUT Higgs field | 1 | 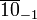 | + | 0 |
| Hu | electroweak Higgs field | 1 | 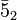 | + | 2 |
| Hd | electroweak Higgs field | 1 | 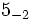 | + | 2 |
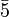 | matter fields | 3 | 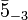 | - | 0 |
| 10 | matter fields | 3 | 101 | - | 0 |
| 1 | left-handed positron | 3 | 15 | - | 0 |
| φ | sterile neutrino (optional) | 3 | 10 | - | 2 |
| S | singlet | 1 | 10 | + | 2 |
Superpotential
A generic invariant renormalizable superpotential is a (complex) 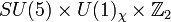 invariant cubic polynomial in the superfields which has an R-charge of 2. It is a linear combination of the following terms:
invariant cubic polynomial in the superfields which has an R-charge of 2. It is a linear combination of the following terms:
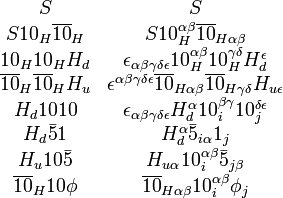
The second column expands each term in index notation (neglecting the proper normalization coefficient). i and j are the generation indices. The coupling Hd 10i 10j has coefficients which are symmetric in i and j.
In those models without the optional φ sterile neutrinos, we add the nonrenormalizable couplings instead.
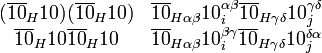
These couplings do break the R-symmetry.
References
- ↑ Barr SM. Phys.Lett. B 112 (1982) 219
- ↑ Derendinger JP, Kim JE, and Nanopoulos DV. Phys.Lett. B 139 (1984) 170
- ↑ Stenger, Victor J., Quantum Gods: Creation, Chaos and the Search for Cosmic Consciouness, Prometheus Books (2009) ISBN 978-1-59102-713-3 p 61.
- ↑ Freedman DH. "The new theory of everything", Discover, 1991, pp 54–61.
- ↑ Rizos J and Tamvakis K. Hierarchical Neutrino Masses and Mixing in Flipped-SU(5). arXiv.org > hep-ph > arXiv:0912.3997v1 (Dec. 20, 2009)
- ↑ Barcow, Timothy et al, Electroweak symmetry breaking and new physics at the TeV scale World Scientific, 1996 ISBN 978-981-02-2631-2 p 194
![\pi _{2}\left({\frac {[SU(5)\times U(1)_{\chi }]/{\mathbb {Z}}_{5}}{[SU(3)\times SU(2)\times U(1)_{Y}]/{\mathbb {Z}}_{6}}}\right)=0](/2014-wikipedia_en_all_02_2014/I/media/0/3/f/2/03f22962244c0329666573caa76525b5.png)