Flexural modulus

From Wikipedia, the free encyclopedia

In mechanics, the flexural modulus or bending modulus[1] is the ratio of stress to strain in flexural deformation, or the tendency for a material to bend. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D 790), and uses units of force per area.[2] It is an intensive property.

For a 3-point test of a rectangular beam behaving as an isotropic linear material, where w and h are the width and height of the beam, L is the distance between the two outer supports and d is the deflection due to the load F applied at the middle of the beam, the flexural modulus:

E_{{{\mathrm {bend}}}}={\frac {L^{3}F}{4wh^{3}d}}

From elastic beam theory 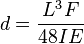d={\frac {L^{3}F}{48IE}} and for rectangular beam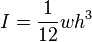 I={\frac {1}{12}}wh^{3}

thus 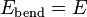E_{{{\mathrm {bend}}}}=E (Elastic modulus)


See also

References

  1. ↑ Modulus in Bending
  2. ↑ Flexural Modulus: Definition


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.