Flat morphism

From Wikipedia, the free encyclopedia

In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,

fP: OY,f(P) → OX,P

is a flat map for all P in X.[1] A map of rings A → B is called flat, if it is a homomorphism that makes B a flat A-module.

A morphism of schemes f is a faithfully flat morphism if f is a surjective flat morphism.[2]

Two of the basic intuitions are that flatness is a generic property, and that the failure of flatness occurs on the jumping set of the morphism.

The first of these comes from commutative algebra: subject to some finiteness conditions on f, it can be shown that there is a non-empty open subscheme Y′ of Y, such that f restricted to Y′ is a flat morphism (generic flatness). Here 'restriction' is interpreted by means of fiber product, applied to f and the inclusion map of Y′ into Y.

For the second, the idea is that morphisms in algebraic geometry can exhibit discontinuities of a kind that are detected by flatness. For instance, the operation of blowing down in the birational geometry of an algebraic surface, can give a single fiber that is of dimension 1 when all the others have dimension 0. It turns out (retrospectively) that flatness in morphisms is directly related to controlling this sort of semicontinuity, or one-sided jumping.

Flat morphisms are used to define (more than one version of) the flat topos, and flat cohomology of sheaves from it. This is a deep-lying theory, and has not been found easy to handle. The concept of étale morphism (and so étale cohomology) depends on the flat morphism concept: an étale morphism being flat, of finite type, and unramified.

Properties of flat morphisms

Let f : X → Y be a morphism of schemes. For a morphism g : Y′ → Y, let X′ = X ×Y Y′ and f′ = f × g : X′ → Y′. f is flat if and only if for every g, the pullback f′* is an exact functor from the category of quasi-coherent 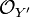{\mathcal {O}}_{{Y'}}-modules to the category of quasi-coherent 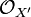{\mathcal {O}}_{{X'}}-modules.[3]

Assume that f : X → Y and g : Y → Z are morphisms of schemes. Assume furthermore that f is flat at x in X. Then g is flat at f(x) if and only if gf is flat at x.[4] In particular, if f is faithfully flat, then g is flat or faithfully flat if and only if gf is flat or faithfully flat, respectively.[5]

Fundamental properties

  • The composite of two flat morphisms is flat.[6]
  • The fibered product of two flat or faithfully flat morphisms is a flat or faithfully flat morphism, respectively.[7]
  • Flatness and faithful flatness is preserved by base change: If f is flat or faithfully flat and g : Y′ → Y, then the fiber product f × g : X ×Y Y′ → Y is flat or faithfully flat, respectively.[8]
  • The set of points where a morphism (locally of finite presentation) is flat is open.[9]
  • If f is faithfully flat and of finite presentation, and if gf is finite type or finite presentation, then g is of finite type or finite presentation, respectively.[10]

Suppose that f: X → Y is a flat morphism of schemes.

  • If F is a quasi-coherent sheaf of finite presentation on Y (in particular, if F is coherent), and if J is the annihilator of F on Y, then 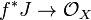f^{*}J\to {\mathcal {O}}_{X}, the pullback of the inclusion map, is an injection, and the image of f*J in 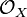{\mathcal {O}}_{X} is the annihilator of f*F on X.[11]
  • If f is faithfully flat and if G is a quasi-coherent {\mathcal {O}}_{Y}-module, then the pullback map on global sections 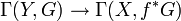\Gamma (Y,G)\to \Gamma (X,f^{*}G) is injective.[12]

Suppose now that h : S′ → S is flat. Let X and Y be S-schemes, and let X′ and Y′ be their base change by h.

  • If f : X → Y is quasi-compact and dominant, then its base change f′ : X′ → Y′ is quasi-compact and dominant.[13]
  • If h is faithfully flat, then the pullback map HomS(X, Y) → HomS′(X′, Y′) is injective.[14]
  • Assume that f : X → Y is quasi-compact and quasi-separated. Let Z be the closed image of X, and let j : Z → Y be the canonical injection. Then the closed subscheme determined by the base change j′ : Z′ → Y′ is the closed image of X′.[15]

Topological properties

If f : X → Y is flat, then it possesses all of the following properties:

  • For every point x of X and every generization y′ of y = f(x), there is a generization x′ of x such that y′ = f(x′).[16]
  • For every point x of X, 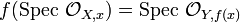f(\operatorname {Spec}\,{\mathcal {O}}_{{X,x}})=\operatorname {Spec}\,{\mathcal {O}}_{{Y,f(x)}}.[17]
  • For every irreducible closed subset Y′ of Y, every irreducible component of f−1(Y′) dominates Y.[18]
  • If Z and Z′ are two irreducible closed subsets of Y with Z contained in Z′, then for every irreducible component T of f−1(Z), there is an irreducible component T′ of f−1(Z′) containing T.[19]
  • For every irreducible component T of X, the closure of f(T) is an irreducible component of Y.[20]
  • If Y is irreducible with generic point y, and if f−1(y) is irreducible, then X is irreducible.[21]
  • If f is also closed, the image of every connected component of X is a connected component of Y.[22]
  • For every pro-constructible subset Z of Y, 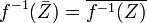f^{{-1}}({\bar Z})=\overline {f^{{-1}}(Z)}.[23]

If f is flat and locally of finite presentation, then f is universally open.[24] However, if f is faithfully flat and quasi-compact, it is not in general true that f is open, even if X and Y are noetherian.[25] Furthermore, no converse to this statement holds: If f is the canonical map from the reduced scheme Xred to X, then f is a universal homeomorphism, but for X noetherian, f is never flat.[26]

If f : X → Y is faithfully flat, then:

  • The topology on Y is the quotient topology relative to f.[27]
  • If f is also quasi-compact, and if Z is a subset of Y, then Z is a locally closed pro-constructible subset of Y if and only if f−1(Z) is a locally closed pro-constructible subset of X.[28]

If f is flat and locally of finite presentation, then for each of the following properties P, the set of points where f has P is open:[29]

  • Serre's condition Sk (for any fixed k).
  • Geometrically regular.
  • Geometrically normal.

If in addition f is proper, then the same is true for each of the following properties:[30]

  • Geometrically reduced.
  • Geometrically reduced and having k geometric connected components (for any fixed k).
  • Geometrically integral.

Flatness and dimension

Assume that X and Y are locally noetherian, and let f : X → Y.

  • Let x be a point of X and y = f(x). If f is flat, then dimx X = dimy Y + dimx f−1(y).[31] Conversely, if this equality holds for all x, X is Cohen–Macaulay, and Y is regular, then f is flat.[32]
  • If f is faithfully flat, then for each closed subset Z of Y, codimY(Z) = codimX(f−1(Z)).[33]
  • Suppose that f is flat and that F is a quasi-coherent module over Y. If F has projective dimension at most n, then f*F has projective dimension at most n.[34]

Descent properties

  • Assume f is flat at x in X. If X is reduced or normal at x, then Y is reduced or normal, respectively, at f(x).[35] Conversely, if f is also of finite presentation and f−1(y) is reduced or normal, respectively, at x, then X is reduced or normal, respectively, at x.[36]
  • In particular, if f is faithfully flat, then X reduced or normal implies that Y is reduced or normal, respectively. If f is faithfully flat and of finite presentation, then all the fibers of f reduced or normal implies that X is reduced or normal, respectively.
  • If f is flat at x in X, and if X is integral or integrally closed at x, then Y is integral or integrally closed, respectively, at f(x).[37]
  • If f is faithfully flat, X is locally integral, and the topological space of Y is locally noetherian, then Y is locally integral.[38]
  • If f is faithfully flat and quasi-compact, and if X is locally noetherian, then Y is also locally noetherian.[39]
  • Assume that f is flat and X and Y are locally noetherian. If X is regular at x, then Y is regular at f(x). Conversely, if Y is regular at f(x) and f−1(f(x)) is regular at x, then X is regular at x.[40]
  • Assume again that f is flat and X and Y are locally noetherian. If X is normal at x, then Y is normal at f(x). Conversely, if Y is normal at f(x) and f−1(f(x)) is normal at x, then X is normal at x.[41]

Let g : Y′ → Y be faithfully flat. Let F be a quasi-coherent sheaf on Y, and let F′ be the pullback of F to Y′. Then F is flat over Y if and only if F′ is flat over Y′.[42]

Assume that f is faithfully flat and quasi-compact. Let G be a quasi-coherent sheaf on Y, and let F denote its pullback to X. Then F is finite type, finite presentation, or locally free of rank n if and only if G has the corresponding property.[43]

Suppose that f : X → Y is an S-morphism of S-schemes. Let g : S′ → S be faithfully flat and quasi-compact, and let X′, Y′, and f′ denote the base changes by g. Then for each of the following properties P, f has P if and only if f′ has P.[44]

  • Open.
  • Universally open.
  • Closed.
  • Universally closed.
  • A homeomorphism.
  • A universal homeomorphism.
  • Quasi-compact.
  • Quasi-compact and universally bicontinuous.
  • Quasi-compact and a homeomorphism onto its image.
  • Quasi-compact and dominant.
  • Separated.
  • Quasi-separated.
  • Locally of finite type.
  • Locally of finite presentation.
  • Finite type.
  • Finite presentation.
  • Proper.
  • An isomorphism.
  • A monomorphism.
  • An open immersion.
  • A quasi-compact immersion.
  • A closed immersion.
  • Affine.
  • Quasi-affine.
  • Finite.
  • Quasi-finite.
  • Integral.

It is possible for f′ to be a local isomorphism without f being even a local immersion.[45]

If f is quasi-compact and L is an invertible sheaf on X, then L is f-ample or f-very ample if and only if its pullback L′ is f′-ample or f′-very ample, respectively.[46] However, it is not true that f is projective if and only if f′ is projective. It is not even true that if f is proper and f′ is projective, then f is quasi-projective, because it is possible to have an f′-ample sheaf on X′ which does not descend to X.[47]

Notes

  1. ↑ EGA IV2, 2.1.1.
  2. ↑ EGA 0I, 6.7.8.
  3. ↑ EGA IV2, Proposition 2.1.3.
  4. ↑ EGA IV2, Corollaire 2.2.11(iv).
  5. ↑ EGA IV2, Corollaire 2.2.13(iii).
  6. ↑ EGA IV2, Corollaire 2.1.6.
  7. ↑ EGA IV2, Corollaire 2.1.7, and EGA IV2, Corollaire 2.2.13(ii).
  8. ↑ EGA IV2, Proposition 2.1.4, and EGA IV2, Corollaire 2.2.13(i).
  9. ↑ EGA IV3, Théorème 11.3.1.
  10. ↑ EGA IV3, Proposition 11.3.16.
  11. ↑ EGA IV2, Proposition 2.1.11.
  12. ↑ EGA IV2, Corollaire 2.2.8.
  13. ↑ EGA IV2, Proposition 2.3.7(i).
  14. ↑ EGA IV2, Corollaire 2.2.16.
  15. ↑ EGA IV2, Proposition 2.3.2.
  16. ↑ EGA IV2, Proposition 2.3.4(i).
  17. ↑ EGA IV2, Proposition 2.3.4(ii).
  18. ↑ EGA IV2, Proposition 2.3.4(iii).
  19. ↑ EGA IV2, Corollaire 2.3.5(i).
  20. ↑ EGA IV2, Corollaire 2.3.5(ii).
  21. ↑ EGA IV2, Corollaire 2.3.5(iii).
  22. ↑ EGA IV2, Proposition 2.3.6(ii).
  23. ↑ EGA IV2, Théorème 2.3.10.
  24. ↑ EGA IV2, Théorème 2.4.6.
  25. ↑ EGA IV2, Remarques 2.4.8(i).
  26. ↑ EGA IV2, Remarques 2.4.8(ii).
  27. ↑ EGA IV2, Corollaire 2.3.12.
  28. ↑ EGA IV2, Corollaire 2.3.14.
  29. ↑ EGA IV3, Théorème 12.1.6.
  30. ↑ EGA IV3, Théorème 12.2.4.
  31. ↑ EGA IV2, Corollaire 6.1.2.
  32. ↑ EGA IV2, Proposition 6.1.5. Note that the regularity assumption on Y is important here. The extension {\mathbb C}[x^{2},y^{2},xy]\subset {\mathbb C}[x,y] gives a counterexample with X regular, Y normal, f finite surjective but not flat.
  33. ↑ EGA IV2, Corollaire 6.1.4.
  34. ↑ EGA IV2, Corollaire 6.2.2.
  35. ↑ EGA IV2, Proposition 2.1.13.
  36. ↑ EGA IV3, Proposition 11.3.13.
  37. ↑ EGA IV2, Proposition 2.1.13.
  38. ↑ EGA IV2, Propostion 2.1.14.
  39. ↑ EGA IV2, Proposition 2.2.14.
  40. ↑ EGA IV2, Corollaire 6.5.2.
  41. ↑ EGA IV2, Corollaire 6.5.4.
  42. ↑ EGA IV2, Proposition 2.5.1.
  43. ↑ EGA IV2, Proposition 2.5.2.
  44. ↑ EGA IV2, Proposition 2.6.2, Corollaire 2.6.4, and Proposition 2.7.1.
  45. ↑ EGA IV2, Remarques 2.7.3(iii).
  46. ↑ EGA IV2, Corollaire 2.7.2.
  47. ↑ EGA IV2, Remarques 2.7.3(ii).

See also

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.