Fixation (population genetics)

From Wikipedia, the free encyclopedia

In population genetics, fixation is the change in a gene pool from a situation where there exists at least two variants of a particular gene (allele) to a situation where only one of the alleles remains.[1] The term can refer to a gene in general or particular nucleotide position in the DNA chain (locus).

In the process of substitution, a previously non-existent allele arises by mutation and undergoes fixation by spreading through the population by random genetic drift and/or positive selection. Once the frequency of the allele is at 100%, i.e. being the only gene variant present in any member, it is said to be "fixed" in the population.[1]

Similarly, genetic differences between taxa are said to have been fixed in each species.

Probability of fixation

Under conditions of genetic drift alone, every finite set of genes or alleles has a "coalescent point" at which all descendants converge to a single ancestor (i.e. they 'coalesce'). This fact can be used to derive the rate of gene fixation of a neutral allele (that is, one not under any form of selection) for a population of varying size (provided that it is finite and nonzero). Because the effect of natural selection is stipulated to be negligible, the probability at any given time that an allele will ultimately become fixed at its locus is simply its frequency p in the population at that time. For example, if a population includes allele A with frequency equal to 20%, and allele a with frequency equal to 80%, there is an 80% chance that after an infinite number of generations a will be fixed at the locus (assuming genetic drift is the only operating evolutionary force).

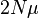For a diploid population of size N and neutral mutation rate \mu , the initial frequency of a novel mutation is simply 1/(2N), and the number of new mutations per generation is 2N\mu . Since the fixation rate is the rate of novel neutral mutation multiplied by their probability of fixation, the overall fixation rate is 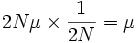2N\mu \times {\frac {1}{2N}}=\mu . Thus, the rate of fixation for a mutation not subject to selection is simply the rate of introduction of such mutations.[2][3]

References

  1. ↑ 1.0 1.1 Arie Zackay (2007). Random Genetic Drift & Gene Fixation. 
  2. ↑ "Probability of fixation". 
  3. ↑ David H.A. Fitch (1997). Deviations from the null hypotheses: Finite populations sizes and genetic drift, mutation and gene flow. 

Further reading

  • Gillespie, J.H. (1994) The Causes of Molecular Evolution. Oxford University Press Inc., USA.
  • Hartl, D.L. and Clark, A.G. (2006) Principles of Population Genetics (4th edition). Sinauer Associates Inc., USA.
  • Kimura, M. (1962) On the Probability of Fixation of Mutant Genes in a Population. Genetics 47: 713–719. PubMed Central
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.