First quantization

From Wikipedia, the free encyclopedia

Quantum mechanics
Introduction Glossary · History
Background Bra–ket notation Classical mechanics Hamiltonian Interference Old quantum theory
Fundamental concepts Complementarity Decoherence Entanglement Energy level Nonlocality Quantum state Superposition Tunnelling Uncertainty Wave function Wave function collapse Symmetry Measurement
Experiments Afshar Bell's inequality Davisson–Germer Delayed choice quantum eraser Double-slit Elitzur-Vaidman Franck-Hertz Mach-Zehnder inter. Popper Quantum eraser Schrödinger's cat Stern–Gerlach Wheeler's delayed choice
Formulations Formulations Heisenberg Interaction Matrix mechanics Schrödinger Sum over histories Phase space
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Interpretations (overview) Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden variables Many-worlds Objective collapse Quantum logic Relational Stochastic Transactional
Advanced topics Quantum chaos Quantum field theory Density matrix Quantum statistical mechanics Quantum information science Quantum computing Scattering theory Fractional quantum mechanics Relativistic quantum mechanics
Scientists Bell Blackett Bohm Bohr Born Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Heisenberg Hilbert Jordan Kramers von Neumann Pauli Lamb Landau Laue Moseley Millikan Onnes Planck Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

A first quantization of a physical system is a semi-classical treatment of quantum mechanics, in which particles or physical objects are treated using quantum wave functions but the surrounding environment (for example a potential well or a bulk electromagnetic field or gravitational field) is treated classically. First quantization is appropriate for studying a single quantum-mechanical system being controlled by a laboratory apparatus that is itself large enough that classical mechanics is applicable to most of the apparatus.

Theoretical background

The starting point is the notion of quantum states and the observables of the system under consideration. Quantum theory postulates that all quantum states are represented by state vectors in a Hilbert space, and that all observables are represented by Hermitian operators acting on that space.^[1] Parallel state vectors represent the same physical state, and therefore one mostly deals with normalized state vectors. Any given Hermitan operator ${\hat {A}}$ has a number of eigenstates 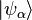$|\psi _{\alpha }\rangle$ that are left invariant by the action of the operator up to a real scale factor $\alpha$ , i. 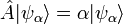e., ${\hat {A}}|\psi _{\alpha }\rangle =\alpha |\psi _{\alpha }\rangle$ . The scale factors are denoted the eigenvalues of the operator. It is a fundamental theorem of Hilbert space theory that the set of all eigenvectors of any given Hermitian operator forms a complete basis set of the Hilbert space.

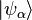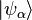In general the eigenstates $|\psi _{\alpha }\rangle$ and $|\psi _{\beta }\rangle$ of two different Hermitian operators ${\hat {A}}$ and ${\hat {B}}$ are not the same. By measurement of the type ${\hat {B}}$ the quantum state can be prepared to be in an eigenstate $|\psi _{\beta }\rangle$ . 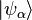This state can also be expressed as a superposition of eigenstates $|\psi _{\alpha }\rangle$ as $|\psi _{\beta }\rangle =\sum _{\alpha }|\psi _{\alpha }\rangle C_{{\alpha \beta }}$ . If one measures the dynamical variable associated with the operator ${\hat {A}}$ in this state, one cannot in general predict the outcome with certainty. It is only described in probabilistic terms. The probability of having any given $|\psi _{\alpha }\rangle$ as the outcome is given as the absolute square 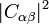$|C_{{\alpha \beta }}|^{2}$ of the associated expansion coefficient. This non-causal element of quantum theory is also known as the wave function collapse. However, between collapse events the time evolution of quantum states is perfectly deterministic.

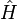The time evolution of a state vector $|\psi (t)\rangle$ is governed by the central operator in quantum mechanics, the Hamiltonian ${\hat {H}}$ (the operator associated with the total energy of the system), through Schrödinger's equation:

$i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle ={\hat H}|\psi (t)\rangle$

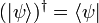Each state vector $|\psi \rangle$ is associated with an adjoint state vector $(|\psi \rangle )^{\dagger }=\langle \psi |$ and can form inner products, "bra(c)kets" $\langle \psi |\phi \rangle$ between adjoint "bra" states $\langle \psi |$ and "ket" states $|\phi \rangle$ . The standard geometrical terminology is used; e.g. the norm squared of $|\psi \rangle$ is given by $\langle \psi |\psi \rangle$ and $|\psi \rangle$ and $|\phi \rangle$ are said to be orthogonal if $\langle \psi |\phi \rangle =0$ . If ${|\psi _{\alpha }\rangle }$ is an orthonormal basis of the Hilbert space, the above-mentioned expansion coefficient $C_{{\alpha \beta }}$ is found forming inner products: $C_{{\alpha \beta }}=\langle \psi _{\alpha }|\psi _{\beta }\rangle$ . A further connection between the direct and the adjoint Hilbert space is given by the relation $\langle \psi |\phi \rangle =\langle \phi |\psi \rangle ^{*}$ , which also leads to the definition of adjoint operators. 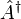For a given operator ${\hat {A}}$ the adjoint operator ${\hat {A}}^{\dagger }$ is defined by demanding $\langle \psi |{\hat {A}}|\phi \rangle =\langle \phi |{\hat {A}}^{\dagger }|\psi \rangle ^{*}$ for any $|\psi \rangle$ and $|\phi \rangle$ .

One-particle systems

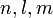In general, the one-particle state could be described by a complete set of quantum numbers denoted by $\nu$ . For example, the three quantum numbers $n,l,m$ associated to an electron in a coulomb potential, like the hydrogen atom, form a complete set (ignoring spin). Hence, the state is called $|\nu \rangle$ and is an eigenvector of the Hamiltonian operator. 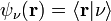One can obtain a state function representation of the state using $\psi _{\nu }({\mathbf {r}})=\langle {\mathbf {r}}|\nu \rangle$ . All eigenvectors of an Hermitian operator form a complete basis, so one can construct any state $|\psi \rangle =\sum _{\nu }|\nu \rangle \langle \nu |\psi \rangle$ obtaining the completeness relation:

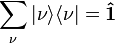
$\sum _{\nu }|\nu \rangle \langle \nu |={\mathbf {{\hat 1}}}$

All the properties of the particle could be known using this vector basis.

Many-particle systems

When turning to N-particle systems, i.e., systems containing N identical particles i.e. particles characterized by the same quantum numbers such as mass, charge and spin, is necessary an extension of single-particle state function $\psi ({\mathbf {r}})$ to the N-particle state function $\psi ({\mathbf {r}}_{1},{\mathbf {r}}_{2},...,{\mathbf {r}}_{N})$ .^[2] A fundamental difference between classical and quantum mechanics concerns the concept of indistinguishability of identical particles. Only two species of particles are thus possible in quantum physics, the so-called bosons and fermions which obey the rules:

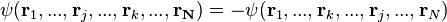$\psi ({\mathbf {r}}_{1},...,{\mathbf {r}}_{j},...,{\mathbf {r}}_{k},...,{\mathbf {r_{N}}})=+\psi ({\mathbf {r}}_{1},...,{\mathbf {r}}_{k},...,{\mathbf {r}}_{j},...,{\mathbf {r}}_{N})$ (bosons),

$\psi ({\mathbf {r}}_{1},...,{\mathbf {r}}_{j},...,{\mathbf {r}}_{k},...,{\mathbf {r_{N}}})=-\psi ({\mathbf {r}}_{1},...,{\mathbf {r}}_{k},...,{\mathbf {r}}_{j},...,{\mathbf {r}}_{N})$ (fermions).

Where we have interchanged two coordinates 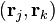$({\mathbf {r}}_{j},{\mathbf {r}}_{k})$ of the state function. The usual wave function is obtained using the slater determinant and the identical particles theory. Using this basis, it is possible to solve any many-particle problem.

References

↑ Dirac, P. A. M. (1982). Principles of Quantum Mechanics. USA: Oxford University Press. ISBN 0-19-852011-5.
↑ Merzbacher, E. (1970). Quamtum mechanics. New York: John Wiley & sons. ISBN 0471887021.

First quantization

Theoretical background

One-particle systems

Many-particle systems

References

See also