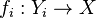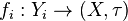Final topology

From Wikipedia, the free encyclopedia

In general topology and related areas of mathematics, the final topology (or strong topology or colimit topology or projective topology) on a set $X$ , with respect to a family of functions into $X$ , is the finest topology on X which makes those functions continuous.

The dual notion is the initial topology.

Definition

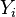Given a set $X$ and a family of topological spaces $Y_{i}$ with functions

$f_{i}:Y_{i}\to X$

the final topology $\tau$ on $X$ is the finest topology such that each

$f_{i}:Y_{i}\to (X,\tau )$

is continuous.

Explicitly, the final topology may be described as follows: a subset U of X is open if and only if 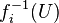$f_{i}^{{-1}}(U)$ is open in Y_i for each i ∈ I.

Examples

The quotient topology is the final topology on the quotient space with respect to the quotient map.
The disjoint union is the final topology with respect to the family of canonical injections.
More generally, a topological space is coherent with a family of subspaces if it has the final topology coinduced by the inclusion maps.
The direct limit of any direct system of spaces and continuous maps is the set-theoretic direct limit together with the final topology determined by the canonical morphisms.
Given a family of topologies {τ_i} on a fixed set X the final topology on X with respect to the functions id_X : (X, τ_i) → X is the infimum (or meet) of the topologies {τ_i} in the lattice of topologies on X. That is, the final topology τ is the intersection of the topologies {τ_i}.
The etale space of a sheaf is topologized by a final topology.

Properties

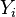A subset of $X$ is closed/open if and only if its preimage under f_i is closed/open in $Y_{i}$ for each i ∈ I.

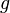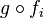The final topology on X can be characterized by the following universal property: a function $g$ from $X$ to some space $Z$ is continuous if and only if $g\circ f_{i}$ is continuous for each i ∈ I.

By the universal property of the disjoint union topology we know that given any family of continuous maps f_i : Y_i → X there is a unique continuous map

$f\colon \coprod _{i}Y_{i}\to X$

If the family of maps f_i covers X (i.e. each x in X lies in the image of some f_i) then the map f will be a quotient map if and only if X has the final topology determined by the maps f_i.

Categorical description

In the language of category theory, the final topology construction can be described as follows. Let Y be a functor from a discrete category J to the category of topological spaces Top which selects the spaces Y_i for i in J. Let Δ be the diagonal functor from Top to the functor category Top^J (this functor sends each space X to the constant functor to X). The comma category (Y ↓ Δ) is then the category of cones from Y, i.e. objects in (Y ↓ Δ) are pairs (X, f) where f_i : Y_i → X is a family of continuous maps to X. If U is the forgetful functor from Top to Set and Δ′ is the diagonal functor from Set to Set^J then the comma category (UY ↓ Δ′) is the category of all cones from UY. The final topology construction can then be described as a functor from (UY ↓ Δ′) to (Y ↓ Δ). This functor is left adjoint to the corresponding forgetful functor.

References

Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (Provides a short, general introduction)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.