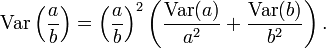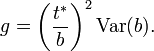Fieller's theorem

From Wikipedia, the free encyclopedia

In statistics, Fieller's theorem allows the calculation of a confidence interval for the ratio of two means.

Approximate confidence interval

Variables a and b may be measured in different units, so there is no way to directly combine the standard errors as they may also be in different units. The most complete discussion of this is given by Fieller (1954).^[1]

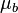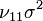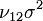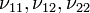Fieller showed that if a and b are (possibly correlated) means of two samples with expectations $\mu _{a}$ and $\mu _{b}$ , and variances $\nu _{{11}}\sigma ^{2}$ and $\nu _{{22}}\sigma ^{2}$ and covariance $\nu _{{12}}\sigma ^{2}$ , and if $\nu _{{11}},\nu _{{12}},\nu _{{22}}$ are all known, then a (1 − α) confidence interval (m_L, m_U) for 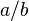$a/b$ is given by

$(m_{L},m_{{U}})={\frac {1}{(1-g)}}\left[{\frac {a}{b}}-{\frac {g\nu _{{12}}}{\nu _{{22}}}}\mp {\frac {t_{{r,\alpha }}s}{b}}{\sqrt {\nu _{{11}}-2{\frac {a}{b}}\nu _{{12}}+{\frac {a^{2}}{b^{2}}}\nu _{{22}}-g\left(\nu _{{11}}-{\frac {\nu _{{12}}^{2}}{\nu _{{22}}}}\right)}}\right]$

where

$g={\frac {t_{{r,\alpha }}^{{2}}s^{2}\nu _{{22}}}{b^{2}}}.$

Here $s^{2}$ is an unbiased estimator of $\sigma ^{2}$ based on r degrees of freedom, and $t_{{r,\alpha }}$ is the $\alpha$ -level deviate from the Student's t-distribution based on r degrees of freedom.

Three features of this formula are important in this context:

a) The expression inside the square root has to be positive, or else the resulting interval will be imaginary.

b) When g is very close to 1, the confidence interval is infinite.

c) When g is greater than 1, the overall divisor outside the square brackets is negative and the confidence interval is exclusive.

Approximate formulae

These equations approximation to the full formula, and are obtained via a Taylor series expansion of a function of two variables and then taking the variance (i.e. a generalisation to two variables of the formula for the approximate standard error for a function of an estimate).

Case 1

Assume that a and b are jointly normally distributed, and that b is not too near zero (i.e. more specifically, that the standard error of b is small compared to b),

$\operatorname {Var}\left({\frac {a}{b}}\right)=\left({\frac {a}{b}}\right)^{{2}}\left({\frac {\operatorname {Var}(a)}{a^{2}}}+{\frac {\operatorname {Var}(b)}{b^{2}}}\right).$

From this a 95% confidence interval can be constructed in the usual way (degrees of freedom for t^* is equal to the total number of values in the numerator and denominator minus 2).

This can be expressed in a more useful form for when (as is usually the case) logged data is used, using the following relation for a function of x and y, say ƒ(x, y):

$\operatorname {Var}(f)=\left({\frac {\partial f}{\partial x}}\right)^{2}\operatorname {Var}(x)+\left({\frac {\partial f}{\partial y}}\right)^{2}\operatorname {Var}(y)+2{\frac {\partial f}{\partial x}}.{\frac {\partial f}{\partial y}}\operatorname {Cov}(x,y)$

to obtain either,

$\operatorname {Var}\left(\log _{e}{\frac {a}{b}}\right)={\frac {\operatorname {Var}(a)}{a^{2}}}+{\frac {\operatorname {Var}(b)}{b^{2}}}$

$\operatorname {Var}\left(\log _{{10}}{\frac {a}{b}}\right)=\left(\log _{{10}}e\right)^{2}\left({\frac {\operatorname {Var}(a)}{a^{2}}}+{\frac {\operatorname {Var}(b)}{b^{2}}}\right).$

Case 2

Assume that a and b are jointly normally distributed, and that b is near zero (i.e. SE(b) is not small compared to b).

First, calculate the intermediate quantity:

$g=\left({\frac {t^{{*}}}{b}}\right)^{{2}}\operatorname {Var}(b).$

You cannot calculate the confidence interval of the quotient if 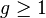$g\geq 1$ , as the CI for the denominator μ_b will include zero.

However if 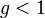$g<1$ then we can obtain

$\operatorname {Var}\left({\frac {a}{b}}\right)=\left({\frac {a}{b(1-g)}}\right)^{{2}}\left((1-g){\frac {\operatorname {Var}(a)}{a^{2}}}+{\frac {\operatorname {Var}(b)}{b^{2}}}\right).$

Other

One problem is that, when g is not small, CIs can blow up when using Fieller's theorem. Andy Grieve has provided a Bayesian solution where the CIs are still sensible, albeit wide.^[2] Bootstrapping provides another alternative that that does not require the assumption of normality.^[3]

History

Edgar C. Fieller (1907–1960) first started working on this problem while in Karl Pearson's group at University College London, where he was employed for five years after graduating in Mathematics from King's College, Cambridge. He then worked for the Boots Pure Drug Company as a statistician and operational researcher before becoming deputy head of operational research at RAF Fighter Command during the Second World War, after which he was appointed the first head of the Statistics Section at the National Physical Laboratory.^[4]

Notes

↑ Fieller, EC. (1954). "Some problems in interval estimation.". Journal of the Royal Statistical Society, Series B 16 (2): 175–185. JSTOR 2984043.
↑ O'Hagan, A., Stevens, JW. and Montmartin, J. (2000). "Inference for the cost-effectiveness acceptability curve and cost-effectiveness ratio.". Pharmacoeconomics 17 (4): 339–49. doi:10.2165/00019053-200017040-00004. PMID 10947489.
↑ Campbell, M. K.; Torgerson, D. J. (1999). "Bootstrapping: estimating confidence intervals for cost-effectiveness ratios". QJM: an International Journal of Medicine 92 (3): 177–182. doi:10.1093/qjmed/92.3.177. Cite uses deprecated parameters (help)
↑ Irwin, J. O. and Rest, E. D. Van (1961). "Edgar Charles Fieller, 1907-1960". Journal of the Royal Statistical Society, Series A (Blackwell Publishing) 124 (2): 275–277. JSTOR 2984155.