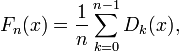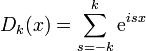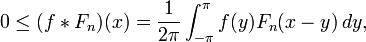Fejér kernel

From Wikipedia, the free encyclopedia

In mathematics, the Fejér kernel is used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity.

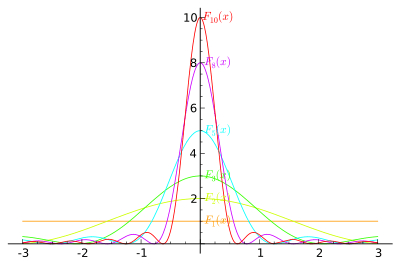
Plot of several Fejér kernels

The Fejér kernel is defined as

$F_{n}(x)={\frac {1}{n}}\sum _{{k=0}}^{{n-1}}D_{k}(x),$

where

$D_{k}(x)=\sum _{{s=-k}}^{k}{{\rm {e}}}^{{isx}}$

is the kth order Dirichlet kernel. It can also be written in a closed form as

$F_{n}(x)={\frac {1}{n}}\left({\frac {\sin {\frac {nx}{2}}}{\sin {\frac {x}{2}}}}\right)^{2}={\frac {1}{n}}{\frac {1-\cos(nx)}{1-\cos x}}$ ,

where this expression is defined.^[1] It is named after the Hungarian mathematician Lipót Fejér (1880–1959).

The important property of the Fejér kernel is 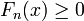$F_{n}(x)\geq 0$ with average value of $1$ . The convolution F_n is positive: for $f\geq 0$ of period $2\pi$ it satisfies

$0\leq (f*F_{n})(x)={\frac {1}{2\pi }}\int _{{-\pi }}^{\pi }f(y)F_{n}(x-y)\,dy,$

and, by Young's inequality,

$\|F_{n}*f\|_{{L^{p}([-\pi ,\pi ])}}\leq \|f\|_{{L^{p}([-\pi ,\pi ])}}$ for every $0\leq p\leq \infty$

for continuous function $f$ ; moreover,

$f*F_{n}\rightarrow f$ for every $f\in L^{p}([-\pi ,\pi ])$ ( $1\leq p<\infty$ )

for continuous function $f$ . Indeed, if $f$ is continuous, then the convergence is uniform.

References

↑ Hoffman, Kenneth (1988). Banach Spaces of Analytic Functions. Dover. p. 17. ISBN 0-486-45874-1.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Fejér kernel

See also

References