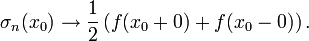Fejér's theorem

From Wikipedia, the free encyclopedia

In mathematics, Fejér's theorem, named for Hungarian mathematician Lipót Fejér, states that if f:R → C is a continuous function with period 2π, then the sequence (σ_n) of Cesàro means of the sequence (s_n) of partial sums of the Fourier series of f converges uniformly to f on [-π,π].

Explicitly,

$s_{n}(x)=\sum _{{k=-n}}^{n}c_{k}e^{{ikx}},$

where

$c_{k}={\frac {1}{2\pi }}\int _{{-\pi }}^{\pi }f(t)e^{{-ikt}}dt,$

and

$\sigma _{n}(x)={\frac {1}{n}}\sum _{{k=0}}^{{n-1}}s_{k}(x)={\frac {1}{2\pi }}\int _{{-\pi }}^{\pi }f(x-t)F_{n}(t)dt,$

with F_n being the nth order Fejér kernel.

A more general form of the theorem applies to functions which are not necessarily continuous (Zygmund 1968, Theorem III.3.4). Suppose that f is in L¹(-π,π). If the left and right limits f(x₀±0) of f(x) exist at x₀, or if both limits are infinite of the same sign, then

$\sigma _{n}(x_{0})\to {\frac {1}{2}}\left(f(x_{0}+0)+f(x_{0}-0)\right).$

Existence or divergence to infinity of the Cesàro mean is also implied. By a theorem of Marcel Riesz, Fejér's theorem holds precisely as stated if the (C, 1) mean σ_n is replaced with (C, α) mean of the Fourier series (Zygmund 1968, Theorem III.5.1).

References

Zygmund, Antoni (1968), Trigonometric series (2nd ed.), Cambridge University Press (published 1988), ISBN 978-0-521-35885-9 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.