Feige–Fiat–Shamir identification scheme

From Wikipedia, the free encyclopedia

In cryptography, the Feige–Fiat–Shamir identification scheme is a type of parallel zero-knowledge proof developed by Uriel Feige, Amos Fiat, and Adi Shamir in 1988. Like all zero-knowledge proofs, the Feige-Fiat-Shamir Identification Scheme allows one party, Peggy, to prove to another party, Victor, that she possesses secret information without revealing to Victor what that secret information is. The Feige-Fiat-Shamir Identification Scheme, however, uses modular arithmetic and a parallel verification process that limits the number of communications between Peggy and Victor.

Setup

Choose two large prime integers p and q and compute the product n = pq. Create secret numbers 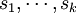$s_{1},\cdots ,s_{k}$ with gcd( $s_{i}$ , $n$ ) = 1. Compute $v_{i}\equiv s_{i}^{{2}}{\pmod {n}}$ . Peggy and Victor both receive $n$ while $p$ and $q$ are kept secret. Peggy is then sent the numbers $s_{i}$ . These are her secret login numbers. Victor is sent the numbers $v_{i}$ . Victor is unable to recover Peggy's $s_{i}$ numbers from his $v_{i}$ numbers due to the difficulty in determining a modular square root when the modulus' factorization is unknown.

Procedure

Peggy chooses a random integer $r$ , a random sign $s\in \{-1,1\}$ and computes $x\equiv s\cdot r^{2}{\pmod {n}}$ . Peggy sends $x$ to Victor.
Victor chooses numbers 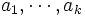$a_{1},\cdots ,a_{k}$ where $a_{i}$ equals 0 or 1. Victor sends these numbers to Peggy.
Peggy computes 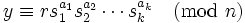$y\equiv rs_{1}^{{a_{1}}}s_{2}^{{a_{2}}}\cdots s_{k}^{{a_{k}}}{\pmod {n}}$ . Peggy sends this number to Victor.
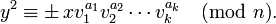
Victor checks that $y^{2}\equiv \pm \,xv_{1}^{{a_{1}}}v_{2}^{{a_{2}}}\cdots v_{k}^{{a_{k}}}{\pmod {n}}.$

This procedure is repeated with different $r$ and $a_{i}$ values until Victor is satisfied that Peggy does indeed possess the modular square roots ( $s_{i}$ ) of his $v_{i}$ numbers.

Security

In the procedure, Peggy does not give any useful information to Victor. She merely proves to Victor that she has the secret numbers without revealing what those numbers are. Anyone who intercepts the communication between each Peggy and Victor would only learn the same information. The eavesdropper would not learn anything useful about Peggy's secret numbers.

In an early version, the Fiat-Shamir-Scheme (on which the Feige-Fiat-Shamir-Scheme was based), one bit of information was leaked. By the introduction of the sign $s$ even this bit was concealed resulting in a zero-knowledge-protocol.

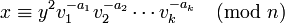Suppose Eve has intercepted Victor's $v_{i}$ numbers but does not know what Peggy's $s_{i}$ numbers are. If Eve wants to try to convince Victor that she is Peggy, she would have to correctly guess what Victor's $a_{i}$ numbers will be. She then picks a random $y$ , calculates $x\equiv y^{2}v_{1}^{{-a_{1}}}v_{2}^{{-a_{2}}}\cdots v_{k}^{{-a_{k}}}{\pmod {n}}$ and sends $x$ to Victor. When Victor sends $a_{i}$ , Eve simply returns her $y$ . Victor is satisfied and concludes that Eve has the secret numbers. However, the probability of Eve correctly guessing what Victor's $a_{i}$ will be is 1 in $2^{k}$ . 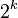By repeating the procedure $t$ times, the probability drops to 1 in 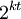$2^{{kt}}$ . 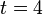For $k=5$ and $t=4$ the probability of successfully posing as Peggy is less than 1 in 1 million.

References

Feige, Uriel; Fiat, Amos; Shamir, Adi (1988). "Zero-knowledge proofs of identity". Journal of Cryptology 1 (2): 77–94. doi:10.1007/BF02351717.
Trappe, Wade; Washington, Lawrence C. (2003). Introduction to Cryptography with Coding Theory. Upper Saddle River: Prentice-Hall. pp. 231–233. ISBN 0-13-061814-4.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.