Feature selection
| Machine learning and data mining |
|---|
 |
| Problems |
| Clustering |
|
| Dimensionality reduction |
|
| Structured prediction |
| Anomaly detection |
|
| Theory |
|
In machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features for use in model construction. The central assumption when using a feature selection technique is that the data contains many redundant or irrelevant features. Redundant features are those which provide no more information than the currently selected features, and irrelevant features provide no useful information in any context. Feature selection techniques are a subset of the more general field of feature extraction. Feature extraction creates new features from functions of the original features, whereas feature selection returns a subset of the features. Feature selection techniques are often used in domains where there are many features and comparatively few samples (or data points). The archetypal case is the use of feature selection in analysing DNA microarrays, where there are many thousands of features, and a few tens to hundreds of samples. Feature selection techniques provide three main benefits when constructing predictive models:
- improved model interpretability,
- shorter training times,
- enhanced generalisation by reducing overfitting.
Feature selection is also useful as part of the data analysis process, as it shows which features are important for prediction, and how these features are related.
Introduction
A feature selection algorithm can be seen as the combination of a search technique for proposing new feature subsets, along with an evaluation measure which scores the different feature subsets. The simplest algorithm is to test each possible subset of features finding the one which minimises the error rate. This is an exhaustive search of the space, and is computationally intractable for all but the smallest of feature sets. The choice of evaluation metric heavily influences the algorithm, and it is these evaluation metrics which distinguish between the three main categories of feature selection algorithms: wrappers, filters and embedded methods.[1]
Wrapper methods use a predictive model to score feature subsets. Each new subset is used to train a model, which is tested on a hold-out set. Counting the number of mistakes made on that hold-out set (the error rate of the model) gives the score for that subset. As wrapper methods train a new model for each subset, they are very computationally intensive, but usually provide the best performing feature set for that particular type of model.
Filter methods use a proxy measure instead of the error rate to score a feature subset. This measure is chosen to be fast to compute, whilst still capturing the usefulness of the feature set. Common measures include the Mutual Information, Pearson product-moment correlation coefficient, and the inter/intra class distance. Filters are usually less computationally intensive than wrappers, but they produce a feature set which is not tuned to a specific type of predictive model. Many filters provide a feature ranking rather than an explicit best feature subset, and the cut off point in the ranking is chosen via cross-validation.
Embedded methods are a catch-all group of techniques which perform feature selection as part of the model construction process. The exemplar of this approach is the LASSO method for constructing a linear model, which penalises the regression coefficients, shrinking many of them to zero. Any features which have non-zero regression coefficients are 'selected' by the LASSO algorithm. One other popular approach is the Recursive Feature Elimination algorithm, commonly used with Support Vector Machines to repeatedly construct a model and remove features with low weights. These approaches tend to be between filters and wrappers in terms of computational complexity.
In statistics, the most popular form of feature selection is stepwise regression. It is a greedy algorithm that adds the best feature (or deletes the worst feature) at each round. The main control issue is deciding when to stop the algorithm. In machine learning, this is typically done by cross-validation. In statistics, some criteria are optimized. This leads to the inherent problem of nesting. More robust methods have been explored, such as branch and bound and piecewise linear network.
Subset selection
Subset selection evaluates a subset of features as a group for suitability. Subset selection algorithms can be broken up into Wrappers, Filters and Embedded. Wrappers use a search algorithm to search through the space of possible features and evaluate each subset by running a model on the subset. Wrappers can be computationally expensive and have a risk of over fitting to the model. Filters are similar to Wrappers in the search approach, but instead of evaluating against a model, a simpler filter is evaluated. Embedded techniques are embedded in and specific to a model.
Many popular search approaches use greedy hill climbing, which iteratively evaluates a candidate subset of features, then modifies the subset and evaluates if the new subset is an improvement over the old. Evaluation of the subsets requires a scoring metric that grades a subset of features. Exhaustive search is generally impractical, so at some implementor (or operator) defined stopping point, the subset of features with the highest score discovered up to that point is selected as the satisfactory feature subset. The stopping criterion varies by algorithm; possible criteria include: a subset score exceeds a threshold, a program's maximum allowed run time has been surpassed, etc.
Alternative search-based techniques are based on targeted projection pursuit which finds low-dimensional projections of the data that score highly: the features that have the largest projections in the lower dimensional space are then selected.
Search approaches include:
- Exhaustive
- Best first
- Simulated annealing
- Genetic algorithm
- Greedy forward selection
- Greedy backward elimination
- Targeted projection pursuit
- Scatter Search[2]
- Variable Neighborhood Search[3]
Two popular filter metrics for classification problems are correlation and mutual information, although neither are true metrics or 'distance measures' in the mathematical sense, since they fail to obey the triangle inequality and thus do not compute any actual 'distance' – they should rather be regarded as 'scores'. These scores are computed between a candidate feature (or set of features) and the desired output category. There are, however, true metrics that are a simple function of the mutual information;[4] see here.
Other available filter metrics include:
- Class separability
- Error probability
- Inter-class distance
- Probabilistic distance
- Entropy
- Consistency-based feature selection
- Correlation-based feature selection
Optimality criteria
There are a variety of optimality criteria that can be used for controlling feature selection. The oldest are Mallows's Cp statistic and Akaike information criterion (AIC). These add variables if the t-statistic is bigger than  .
.
Other criteria are Bayesian information criterion (BIC) which uses 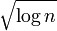 , minimum description length (MDL) which asymptotically uses
, minimum description length (MDL) which asymptotically uses 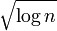 , Bonnferroni / RIC which use
, Bonnferroni / RIC which use  , maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rate (FDR) which use something close to
, maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rate (FDR) which use something close to 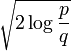 .
.
Minimum-redundancy-maximum-relevance (mRMR) feature selection
Peng et al.[5] proposed an mRMR feature-selection method that can use either mutual information, correlation, distance/similarity scores to select features. For example, with mutual information, relevant features and redundant features are considered simultaneously. The relevance of a feature set S for the class c is defined by the average value of all mutual information values between the individual feature fi and the class c as follows:
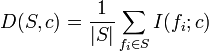 .
.
The redundancy of all features in the set S is the average value of all mutual information values between the feature fi and the feature fj:
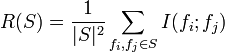
The mRMR criterion is a combination of two measures given above and is defined as follows:
![{\mathrm {mRMR}}=\max _{{S}}\left[{\frac {1}{|S|}}\sum _{{f_{{i}}\in S}}I(f_{{i}};c)-{\frac {1}{|S|^{{2}}}}\sum _{{f_{{i}},f_{{j}}\in S}}I(f_{{i}};f_{{j}})\right].](/2014-wikipedia_en_all_02_2014/I/media/4/0/a/f/40afec7e6c1e3406187b4585fa0381ae.png)
Suppose that there are n full-set features. Let xi be the set membership indicator function for feature fi, so that xi=1 indicates presence and xi=0 indicates absence of the feature fi in the globally optimal feature set. Let ci=I(fi;c) and aij=I(fi;fj). The above may then be written as an optimization problem:
![{\mathrm {mRMR}}=\max _{{x\in \{0,1\}^{{n}}}}\left[{\frac {\sum _{{i=1}}^{{n}}c_{{i}}x_{{i}}}{\sum _{{i=1}}^{{n}}x_{{i}}}}-{\frac {\sum _{{i,j=1}}^{{n}}a_{{ij}}x_{{i}}x_{{j}}}{(\sum _{{i=1}}^{{n}}x_{{i}})^{{2}}}}\right].](/2014-wikipedia_en_all_02_2014/I/media/f/b/e/f/fbef87779d6c6fdf9da9e223eb181419.png)
It may be shown that mRMR feature selection is an approximation of the theoretically optimal maximum-dependency feature selection that maximizes the mutual information between the joint distribution of the selected features and the classification variable. However, since mRMR turned a combinatorial problem as a series of much smaller scale problems, each of which only involves two variables, the estimation of joint probabilities is much more robust. In certain situations the algorithm may underestimate the usefulness of features as it has no way to measure interactions between features. This can lead to poor performance[6] when the features are individually useless, but are useful when combined (a pathological case is found when the class is a parity function of the features). Overall the algorithm is more efficient (in terms of the amount of data required) than the theoretically optimal max-dependency selection, yet produces a low redundancy feature set.
The mRMR method has also been combined with the wrapper methods, thus a wrapper method can be utilized at a smaller cost. It can be seen that mRMR is also related to the correlation based feature selection below. It may also be seen a special case of some generic feature selectors.[7]
Correlation feature selection
The Correlation Feature Selection (CFS) measure evaluates subsets of features on the basis of the following hypothesis: "Good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other".[8] [9] The following equation gives the merit of a feature subset S consisting of k features:
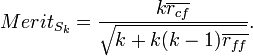
Here, 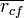 is the average value of all feature-classification correlations, and
is the average value of all feature-classification correlations, and 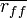 is the average value of all feature-feature correlations. The CFS criterion is defined as follows:
is the average value of all feature-feature correlations. The CFS criterion is defined as follows:
![{\mathrm {CFS}}=\max _{{S_{k}}}\left[{\frac {r_{{cf_{1}}}+r_{{cf_{2}}}+\cdots +r_{{cf_{k}}}}{{\sqrt {k+2(r_{{f_{1}f_{2}}}+\cdots +r_{{f_{i}f_{j}}}+\cdots +r_{{f_{k}f_{1}}})}}}}\right].](/2014-wikipedia_en_all_02_2014/I/media/0/b/0/1/0b01c8f5a4f04c980aaf068f7d093f22.png)
The 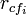 and
and 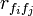 variables are referred to as correlations, but are not necessarily Pearson's correlation coefficient or Spearman's ρ. Dr. Mark Hall's dissertation uses neither of these, but uses three different measures of relatedness, minimum description length (MDL), symmetrical uncertainty, and relief.
variables are referred to as correlations, but are not necessarily Pearson's correlation coefficient or Spearman's ρ. Dr. Mark Hall's dissertation uses neither of these, but uses three different measures of relatedness, minimum description length (MDL), symmetrical uncertainty, and relief.
Let xi be the set membership indicator function for feature fi; then the above can be rewritten as an optimization problem:
![{\mathrm {CFS}}=\max _{{x\in \{0,1\}^{{n}}}}\left[{\frac {(\sum _{{i=1}}^{{n}}a_{{i}}x_{{i}})^{{2}}}{\sum _{{i=1}}^{{n}}x_{i}+\sum _{{i\neq j}}2b_{{ij}}x_{i}x_{j}}}\right].](/2014-wikipedia_en_all_02_2014/I/media/4/7/0/9/470906caccc384e21c788dfd9b2def0d.png)
The combinatorial problems above are, in fact, mixed 0–1 linear programming problems that can be solved by using branch-and-bound algorithms.[10]
General L1-norm support vector machine for feature selection
It has been shown in[11] that the traditional L1-norm SVM proposed by Bradley and Mangasarian in[12] can be generalized to a general L1-norm SVM (GL1-SVM).
Moreover, it has been proved that solving the new proposed optimization problem (GL1-SVM) gives smaller error penalty and enlarges the margin between two support vector hyper-planes, thus possibly gives better generalization capability of SVM than solving the traditional L1-norm SVM.
GL1-SVM may also be seen a special case of some generic feature selectors.[7]
Regularized trees
The features from a decision tree or a tree ensemble are shown to be redundant. A recent method called regularized tree[13] can be used for feature subset selection. Regularized trees penalize using a variable similar to the variables selected at previous tree nodes for splitting the current node. Regularized trees only need build one tree model (or one tree ensemble model) and thus are computationally efficient.
Regularized trees naturally handle numerical and categorical features, interactions and nonlinearities. They are invariant to attribute scales (units) and insensitive to outliers, and thus, require little data preprocessing such as normalization. Regularized random forest (RRF) (RRF) is one type of regularized trees. The guided RRF is an enhanced RRF which is guided by the importance scores from an ordinary random forest.
Embedded methods incorporating feature selection
- Random multinomial logit (RMNL)
- Sparse regression, LASSO
- Regularized trees e.g. regularized random forest implemented in the RRF package
- Decision tree
- Memetic algorithm
- Auto-encoding networks with a bottleneck-layer
- Many other machine learning methods applying a pruning step.
Software for feature selection
Many standard data analysis software systems are often used for feature selection, such as SciLab, NumPy and the R language. Other software systems are tailored specifically to the feature-selection task:
- Weka – freely available and open-source software in Java.
- Feature Selection Toolbox 3 – freely available and open-source software in C++.
- RapidMiner – freely available and open-source software.
- Orange – freely available and open-source software (module orngFSS).
- TOOLDIAG Pattern recognition toolbox – freely available C toolbox.
- minimum redundancy feature selection tool – freely available C/Matlab codes for selecting minimum redundant features.
- A C# Implementation of greedy forward feature subset selection for various classifiers (e.g., LibLinear, SVM-light).
- MCFS-ID (Monte Carlo Feature Selection and Interdependency Discovery) is a Monte Carlo method-based tool for feature selection. It also allows for the discovery of interdependencies between the relevant features. MCFS-ID is particularly suitable for the analysis of high-dimensional, ill-defined transactional and biological data.
- RRF is an R package for feature selection and can be installed from R. RRF stands for Regularized Random Forest, which is a type of Regularized Trees. By building a regularized random forest, a compact set of non-redundant features can be selected without loss of predictive information. Regularized trees can capture non-linear interactions between variables, and naturally handle different scales, and numerical and categorical variables.
See also
References
- ↑ http://jmlr.csail.mit.edu/papers/v3/guyon03a.html
- ↑ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving feature subset selection problem by a Parallel Scatter Search, European Journal of Operational Research, vol. 169, no. 2, pp. 477–489, 2006.
- ↑ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving Feature Subset Selection Problem by a Hybrid Metaheuristic. In First International Workshop on Hybrid Metaheuristics, pp. 59–68, 2004.
- ↑ Alexander Kraskov, Harald Stögbauer, Ralph G. Andrzejak, and Peter Grassberger, "Hierarchical Clustering Based on Mutual Information", (2003) ArXiv q-bio/0311039
- ↑ Peng, H. C.; Long, F.; Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (8): 1226–1238. doi:10.1109/TPAMI.2005.159. PMID 16119262. Program
- ↑ Brown, G., Pocock, A., Zhao, M.-J., Lujan, M. (2012). "Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection", In the Journal of Machine Learning Research (JMLR).
- ↑ 7.0 7.1 Nguyen, H., Franke, K., Petrovic, S. (2010). "Towards a Generic Feature-Selection Measure for Intrusion Detection", In Proc. International Conference on Pattern Recognition (ICPR), Istanbul, Turkey.
- ↑ M. Hall 1999, Correlation-based Feature Selection for Machine Learning
- ↑ Senliol, Baris, et al. "Fast Correlation Based Filter (FCBF) with a different search strategy." Computer and Information Sciences, 2008. ISCIS'08. 23rd International Symposium on. IEEE, 2008.
- ↑ Hai Nguyen, Katrin Franke, and Slobodan Petrovic, Optimizing a class of feature selection measures, Proceedings of the NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML), Vancouver, Canada, December 2009.
- ↑ Nguyen, H. T., Franke, K., Petrovic, S. (2011). "On General Definition of L1-norm Support-Vector Machine for Feature Selection". In Proceedings of the International Journal of Machine Learning and Computing, ISSN: 2010-3700.
- ↑ Bradley, P. & Mangasarian, O.L., (1998). Feature selection via concave minimization and support vector machines. In Proceedings of the Fifteenth International Conference (ICML), pp. 82–90.
- ↑ H. Deng, G. Runger, "Feature Selection via Regularized Trees", Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), IEEE, 2012
Further reading
- Tutorial Outlining Feature Selection Algorithms, Arizona State University
- JMLR Special Issue on Variable and Feature Selection
- Feature Selection for Knowledge Discovery and Data Mining (Book)
- An Introduction to Variable and Feature Selection (Survey)
- Toward integrating feature selection algorithms for classification and clustering (Survey)
- Efficient Feature Subset Selection and Subset Size Optimization (Survey, 2010)
- Searching for Interacting Features
- Feature Subset Selection Bias for Classification Learning
- Y. Sun, S. Todorovic, S. Goodison, Local Learning Based Feature Selection for High-dimensional Data Analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 32, no. 9, pp. 1610–1626, 2010.
External links
- Feature Selection Package, Arizona State University (Matlab Code)
- NIPS challenge 2003 (see also NIPS)
- Naive Bayes implementation with feature selection in Visual Basic (includes executable and source code)
- Minimum-redundancy-maximum-relevance (mRMR) feature selection program
- FEAST (Open source Feature Selection algorithms in C and MATLAB)