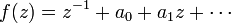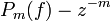Faber polynomials
From Wikipedia, the free encyclopedia
In mathematics, the Faber polynomials Pm of a Laurent series
are the polynomials such that
vanishes at z=0. They were introduced by Faber (1903, 1919) and studied by Grunsky (1939) and Schur (1945).
References
- Curtiss, J. H. (1971), "Faber Polynomials and the Faber Series", The American Mathematical Monthly (Mathematical Association of America) 78 (6): 577–596, ISSN 0002-9890, JSTOR 2316567
- Faber, Georg (1903), "Über polynomische Entwickelungen", Mathematische Annalen (Springer Berlin / Heidelberg) 57: 389–408, doi:10.1007/BF01444293, ISSN 0025-5831
- Faber, G. (1919), "Über Tschebyscheffsche Polynome.", Journal für die reine und angewandte Mathematik (in German) 150: 79–106, ISSN 0075-4102, JFM 47.0315.01
- Grunsky, Helmut (1939), "Koeffizientenbedingungen für schlicht abbildende meromorphe Funktionen", Mathematische Zeitschrift 45 (1): 29–61, doi:10.1007/BF01580272, ISSN 0025-5874
- Schur, Issai (1945), "On Faber polynomials", American Journal of Mathematics 67: 33–41, ISSN 0002-9327, JSTOR 2371913, MR 0011740
- Suetin, P. K. (1998) [1984], Series of Faber polynomials, Analytical Methods and Special Functions 1, New York: Gordon and Breach Science Publishers, ISBN 978-90-5699-058-9, MR 1676281
- Suetin, P. K. (2001), "f/f038010", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.