F-theory

String theory
Fundamental objects String Brane D-brane
Perturbative string theory Bosonic string theory Superstring theory Type I string theory Type II string theory (Type IIA Type IIB) Heterotic string theory (SO(32) heterotic E8xE8 heterotic)
Non-perturbative results S-duality T-duality U-duality Mirror symmetry M-theory AdS/CFT correspondence
Phenomenology String phenomenology String cosmology String theory landscape
Mathematics Mirror symmetry Vertex operator algebras
Related concepts Conformal field theory Holographic principle Kaluza–Klein theory Quantum gravity Supergravity Supersymmetry Theory of Everything Twistor string theory
Theorists Arkani-Hamed Banks Dijkgraaf Duff Fischler Gates Gliozzi Green Greene Gross Gubser Harvey Hořava Kaku Klebanov Kontsevich Maldacena Mandelstam Martinec Minwalla Moore Motl Nekrasov Neveu Olive Polchinski Polyakov Randall Ramond Rohm Scherk Schwarz Seiberg Sen Sơn Strominger Sundrum Susskind 't Hooft Townsend Vafa Veneziano E. Verlinde H. Verlinde Witten Yau Zaslow
History Glossary
v t e

F-theory is a branch of string theory developed by Cumrun Vafa.^[1] The new vacua described as F-theory were discovered by Vafa, and it^[clarify] also allowed string theorists to construct new realistic vacua — in the form of F-theory compactified on elliptically fibered Calabi–Yau four-folds. The letter "F" supposedly stands for "Father".^[2]

Compactifications

F-theory is formally a 12-dimensional theory, but the only way to obtain an acceptable background is to compactify this theory on a two-torus. By doing so, one obtains type IIB superstring theory in 10 dimensions. The SL(2,Z) S-duality symmetry of the resulting type IIB string theory is manifest because it arises as the group of large diffeomorphisms of the two-dimensional torus.

More generally, one can compactify F-theory on an elliptically fibered manifold (elliptic fibration), i.e. a fiber bundle whose fiber is a two-dimensional torus (also called an elliptic curve). For example, a subclass of the K3 manifolds is elliptically fibered, and F-theory on a K3 manifold is dual to heterotic string theory on a two-torus. (Eight dimensions are large.)

The well-known large number of semirealistic solutions to string theory referred to as the string theory landscape, with 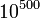elements or so, is dominated by F-theory compactifications on Calabi–Yau four-folds.

Phenomenology

New models of unification of the fundamental forces have recently been developed using F-theory.^[3]

Extra time dimensions

F-theory, as it has metric signature (11,1), as needed for the Euclidean interpretation of the compactification spaces (e.g. the four-folds), is not a "two-time" theory of physics.

However, the signature of the two additional dimensions is somewhat ambiguous due to their infinitesimal character. For example, the supersymmetry of F-theory on a flat background corresponds to type IIB (i.e. (2,0)) supersymmetry with 32 real supercharges which may be interpreted as the dimensional reduction of the chiral real 12-dimensional supersymmetry if its spacetime signature is (10,2). In (11,1) dimensions, the minimum number of components would be 64.

See also

• Dilaton
• Axion

References