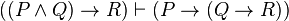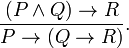Exportation (logic)

From Wikipedia, the free encyclopedia

Transformation rules
Propositional calculus
Rules of inference Modus ponens Modus tollens Biconditional introduction Biconditional elimination Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Absorption Rules of replacement Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Material equivalence Exportation Tautology
Predicate logic
Universal generalization Universal instantiation Existential generalization Existential instantiation
v t e

Exportation^[1]^[2]^[3]^[4] is a valid rule of replacement in propositional logic. The rule allows conditional statements having conjunctive antecedents to be replaced by statements having conditional consequents and vice-versa in logical proofs. It is the rule that:

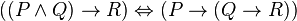
$((P\land Q)\to R)\Leftrightarrow (P\to (Q\to R))$

Where " $\Leftrightarrow$ " is a metalogical symbol representing "can be replaced in a proof with."

Formal notation

The exportation rule may be written in sequent notation:

$((P\land Q)\to R)\vdash (P\to (Q\to R))$

where $\vdash$ is a metalogical symbol meaning that $(P\to (Q\to R))$ is a syntactic consequence of $((P\land Q)\to R)$ in some logical system;

or in rule form:

${\frac {(P\land Q)\to R}{P\to (Q\to R)}}.$

where the rule is that wherever an instance of " $(P\land Q)\to R$ " appears on a line of a proof, it can be replaced with " $P\to (Q\to R)$ ";

or as the statement of a truth-functional tautology or theorem of propositional logic:

$((P\land Q)\to R))\to (P\to (Q\to R)))$

where $P$ , $Q$ , and $R$ are propositions expressed in some logical system.

Natural language

Truth values

At any time, if P→Q is true, it can be replaced by P→(P∧Q).
One possible case for P→Q is for P to be true and Q to be true; thus P∧Q is also true, and P→(P∧Q) is true.
Another possible case sets P as false and Q as true. Thus, P∧Q is false and P→(P∧Q) is false; false→false is true.
The last case occurs when both P and Q are false. Thus, P∧Q is false and P→(P∧Q) is true.

Example

It rains and the sun shines implies that there is a rainbow.
Thus, if it rains, then the sun shines implies that there is a rainbow.

Relation to functions

Exportation is associated with Currying via the Curry–Howard correspondence.

References

↑ Hurley, Patrick (1991). A Concise Introduction to Logic 4th edition. Wadsworth Publishing. pp. 364–5.
↑ Copi, Irving M.; Cohen, Carl (2005). Introduction to Logic. Prentice Hall. p. 371.
↑ Moore and Parker
↑ http://www.philosophypages.com/lg/e11b.htm

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.