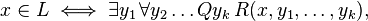Exponential hierarchy

From Wikipedia, the free encyclopedia

In computational complexity theory, the exponential hierarchy is a hierarchy of complexity classes, which is an exponential time analogue of the polynomial hierarchy. As elsewhere in complexity theory, “exponential” is used in two different meanings (linear exponential bounds 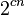$2^{{cn}}$ for a constant c, and full exponential bounds $2^{{n^{c}}}$ ), leading to two versions of the exponential hierarchy:^[1]^[2]

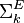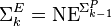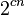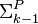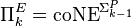EH is the union of the classes $\Sigma _{k}^{E}$ for all k, where $\Sigma _{k}^{E}={\mathrm {NE}}^{{\Sigma _{{k-1}}^{P}}}$ (i.e., languages computable in nondeterministic time $2^{{cn}}$ for some constant c with a $\Sigma _{{k-1}}^{P}$ oracle). One also defines $\Pi _{k}^{E}={\mathrm {coNE}}^{{\Sigma _{{k-1}}^{P}}}$ , $\Delta _{k}^{E}={\mathrm E}^{{\Sigma _{{k-1}}^{P}}}$ . 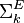An equivalent definition is that a language L is in $\Sigma _{k}^{E}$ if and only if it can be written in the form

$x\in L\iff \exists y_{1}\,\forall y_{2}\dots Qy_{k}\,R(x,y_{1},\dots ,y_{k}),$

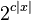where $R(x,y_{1},\dots ,y_{n})$ is a predicate computable in time $2^{{c|x|}}$ (which implicitly bounds the length of y_i). Also equivalently, EH is the class of languages computable on an alternating Turing machine in time 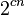$2^{{cn}}$ for some c with constantly many alternations.

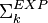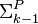EXPH is the union of the classes $\Sigma _{k}^{{EXP}}$ , where $\Sigma _{k}^{{EXP}}={\mathrm {NEXP}}^{{\Sigma _{{k-1}}^{P}}}$ (languages computable in nondeterministic time $2^{{n^{c}}}$ for some constant c with a $\Sigma _{{k-1}}^{P}$ oracle), and again 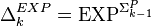$\Pi _{k}^{{EXP}}={\mathrm {coNEXP}}^{{\Sigma _{{k-1}}^{P}}}$ , $\Delta _{k}^{{EXP}}={\mathrm {EXP}}^{{\Sigma _{{k-1}}^{P}}}$ . A language L is in 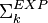$\Sigma _{k}^{{EXP}}$ if and only if it can be written as

$x\in L\iff \exists y_{1}\,\forall y_{2}\dots Qy_{k}\,R(x,y_{1},\dots ,y_{k}),$

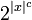where $R(x,y_{1},\dots ,y_{k})$ is computable in time $2^{{|x|^{c}}}$ for some c, which again implicitly bounds the length of y_i. Equivalently, EXPH is the class of languages computable in time $2^{{n^{c}}}$ on an alternating Turing machine with constantly many alternations.

We have E ⊆ NE ⊆ EH ⊆ ESPACE, EXP ⊆ NEXP ⊆ EXPH ⊆ EXPSPACE, and EH ⊆ EXPH.

References

↑ Sarah Mocas, Separating classes in the exponential-time hierarchy from classes in PH, Theoretical Computer Science 158 (1996), no. 1–2, pp. 221–231.
↑ Anuj Dawar, Georg Gottlob, Lauri Hella, Capturing relativized complexity classes without order, Mathematical Logic Quarterly 44 (1998), no. 1, pp. 109–122.

External links

Complexity Zoo: Class EH

v t e Important complexity classes (more)

Considered feasible	DLOGTIME AC⁰ ACC⁰ TC⁰ L SL RL NL NC SC CC P P-complete ZPP RP BPP BQP

Suspected infeasible	UP NP NP-complete NP-hard co-NP co-NP-complete AM PH ⊕P PP #P #P-complete IP PSPACE PSPACE-complete

Considered infeasible	EXPTIME NEXPTIME EXPSPACE ELEMENTARY PR R RE ALL

Class hierarchies	Polynomial hierarchy Exponential hierarchy Grzegorczyk hierarchy Arithmetical hierarchy Boolean hierarchy

Families of classes	DTIME NTIME DSPACE NSPACE Probabilistically checkable proof Interactive proof system

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.