Expander walk sampling

From Wikipedia, the free encyclopedia

In the mathematical discipline of graph theory, the expander walk sampling theorem states that sampling vertices in an expander graph by doing a random walk is almost as good as sampling the vertices independently from a uniform distribution. The earliest version of this theorem is due to Ajtai, Komlós & Szemerédi (1987), and the more general version is typically attributed to Gillman (1998).

Statement

Let $G=(V,E)$ be an expander graph with normalized second-largest eigenvalue 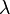$\lambda$ . Let $n$ denote the number of vertices in $G$ . Let $f:V\rightarrow [0,1]$ be a function on the vertices of $G$ . Let $\mu =E[f]$ denote the true mean of $f$ , i.e. $\mu ={\frac {1}{n}}\sum _{{v\in V}}f(v)$ . 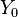Then, if we let $Y_{0},Y_{1},\ldots ,Y_{k}$ denote the vertices encountered in a $k$ -step random walk on $G$ starting at a random vertex $Y_{0}$ , we have the following for all $\gamma >0$ :

$\Pr \left[{\frac {1}{k}}\sum _{{i=0}}^{k}f(Y_{i})-\mu >\gamma \right]\leq e^{{-\Omega (\gamma ^{2}(1-\lambda )k)}}.$

Here the $\Omega$ hides an absolute constant $\geq 1/10$ . An identical bound holds in the other direction:

$\Pr \left[{\frac {1}{k}}\sum _{{i=0}}^{k}f(Y_{i})-\mu <-\gamma \right]\leq e^{{-\Omega (\gamma ^{2}(1-\lambda )k)}}.$

Uses

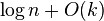This theorem is useful in randomness reduction in the study of derandomization. Sampling from an expander walk is an example of a randomness-efficient sampler. Note that the number of bits used in sampling $k$ independent samples from $f$ is $k\log n$ , whereas if we sample from an infinite family of constant-degree expanders this costs only $\log n+O(k)$ . Such families exist and are efficiently constructible, e.g. the Ramanujan graphs of Lubotzky-Phillips-Sarnak.

Notes

References

Ajtai, M.; Komlós, J.; Szemerédi, E. (1987), Deterministic simulation in LOGSPACE, "Proceedings of the nineteenth annual ACM symposium on Theory of computing", ACM: 132–140, doi:10.1145/28395.28410
Gillman, D. (1998), "A Chernoff Bound for Random Walks on Expander Graphs", SIAM Journal on Computing (Society for Industrial and Applied Mathematics) 27 (4,): 1203–1220, doi:10.1137/S0097539794268765

External links

Proofs of the expander walk sampling theorem.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.