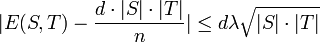Expander mixing lemma
From Wikipedia, the free encyclopedia
The expander mixing lemma states that, for any two subsets 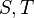 of a d-regular expander graph
of a d-regular expander graph  , the number of edges between
, the number of edges between 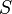 and
and  is approximately what you would expect in a random d-regular graph, i.e.
is approximately what you would expect in a random d-regular graph, i.e.  .
.
Statement
Let  be a d-regular graph with normalized second-largest eigenvalue
be a d-regular graph with normalized second-largest eigenvalue 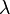 (in absolute value) of the adjacency matrix. Then for any two subsets
(in absolute value) of the adjacency matrix. Then for any two subsets  , let
, let 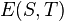 denote the number of edges between S and T.
If the two sets are not disjoint, edges in their intersection are counted twice, that is,
denote the number of edges between S and T.
If the two sets are not disjoint, edges in their intersection are counted twice, that is,
![E(S,T)=2|E(G[S\cap T])|+E(S\setminus T,T)+E(S,T\setminus S)](/2014-wikipedia_en_all_02_2014/I/media/d/f/c/b/dfcb34cd1f8e1e32599c865564305eef.png) .
We have
.
We have
For a proof, see references.
Converse
Recently, Bilu and Linial showed that the converse holds as well: if a graph satisfies the conclusion of the expander mixing lemma, that is, for any two subsets  ,
,
then its second-largest eigenvalue is  .
.
References
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.