Existential instantiation

From Wikipedia, the free encyclopedia

Transformation rules
Propositional calculus
Rules of inference Modus ponens Modus tollens Biconditional introduction Biconditional elimination Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Absorption Rules of replacement Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Material equivalence Exportation Tautology
Predicate logic
Universal generalization Universal instantiation Existential generalization Existential instantiation
v t e

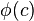In predicate logic, existential instantiation^[1]^[2]^[3] is a valid rule of inference which says that, given a formula of the form $(\exists x)\phi (x)$ , one may infer $\phi (c)$ for a new constant or variable symbol c. The rule has the restriction that the constant or variable c introduced by the rule must be a new term that has not occurred earlier in the proof.

In one formal notation, the rule may be denoted

( $\exists$ x) ${\mathcal {F}}$ x :: ${\mathcal {F}}$ a,

where a is an arbitrary term that has not been a part of our proof thus far.

References

↑ Hurley, Patrick. A Concise Introduction to Logic. Wadsworth Pub Co, 2008.
↑ Copi and Cohen
↑ Moore aand Parker

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Existential instantiation

See also

References