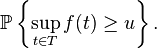Excursion probability

From Wikipedia, the free encyclopedia

In probability theory, an excursion probability is the probability that a stochastic process surpasses a given value in a fixed time period. It is the probability[1]

{\mathbb P}\left\{\sup _{{t\in T}}f(t)\geq u\right\}.

Numerous approximation methods for the situation where u is large and f(t) is a Gaussian process have been proposed such as Rice's formula.[1][2] First-excursion probabilities can be used to describe deflection to a critical point experienced by structures during "random loadings, such as earthquakes, strong gusts, hurricanes, etc."[3]

References

  1. ↑ 1.0 1.1 Adler, Robert J.; Taylor, Jonathan E. (2007). "Excursion Probabilities". Random Fields and Geometry. Springer Monographs in Mathematics. pp. 75–76. doi:10.1007/978-0-387-48116-6_4. ISBN 978-0-387-48112-8. 
  2. ↑ Adler, R. J. (2000). "On excursion sets, tube formulas and maxima of random fields". The Annals of Applied Probability 10: 1. doi:10.1214/aoap/1019737664. JSTOR 2667187. 
  3. ↑ Yang, J. -N. (1973). "First-excursion probability in non-stationary random vibration". Journal of Sound and Vibration 27 (2): 165–182. doi:10.1016/0022-460X(73)90059-X. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.