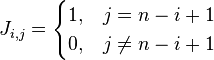Exchange matrix

From Wikipedia, the free encyclopedia

In mathematics, especially linear algebra, the exchange matrix is a special case of a permutation matrix, where the 1 elements reside on the counterdiagonal and all other elements are zero. In other words, it is a 'row-reversed' or 'column-reversed' version of the identity matrix.

$J_{{2}}={\begin{pmatrix}0&1\\1&0\end{pmatrix}};\quad J_{{3}}={\begin{pmatrix}0&0&1\\0&1&0\\1&0&0\end{pmatrix}};\quad J_{{n}}={\begin{pmatrix}0&0&\cdots &0&0&1\\0&0&\cdots &0&1&0\\0&0&\cdots &1&0&0\\\vdots &\vdots &&\vdots &\vdots &\vdots \\0&1&\cdots &0&0&0\\1&0&\cdots &0&0&0\end{pmatrix}}.$

Definition

If J is an n×n exchange matrix, then the elements of J are defined such that:

$J_{{i,j}}={\begin{cases}1,&j=n-i+1\\0,&j\neq n-i+1\\\end{cases}}$

Properties

J^T = J.
Jⁿ = I for even n; Jⁿ = J for odd n, where n is any integer. Thus J is an involutary matrix; that is, J⁻¹ = J.
The trace of J is 1 if n is odd, and 0 if n is even.

Relationships

Any matrix A satisfying the condition AJ = JA is said to be centrosymmetric.
Any matrix A satisfying the condition AJ = JA^T is said to be persymmetric.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.