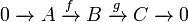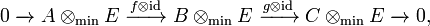Exact C*-algebra
From Wikipedia, the free encyclopedia
In mathematics, an exact C*-algebra is a C*-algebra that preserves exact sequences under the minimum tensor product.
Definition
A C*-algebra E is exact if, for any short exact sequence,
the sequence
where ⊗min denotes the minimum tensor product, is also exact.
Properties
Exact C*-algebras have the following equivalent characterizations:
- A C*-algebra A is exact if and only if A is nuclearly embeddable into B(H), the C*-algebra of all bounded operators on a Hilbert space H.
- A separable C*-algebra A is exact if and only if it is isomorphic to a subalgebra of the Cuntz algebra
 .
.
All nuclear C*-algebras and their C*-subalgebras are exact.
References
- Brown, Nathanial P.; Ozawa, Narutaka (2008). C*-algebras and Finite-Dimensional Approximations. Providence: AMS. ISBN 978-0-8218-4381-9.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.