Even-hole-free graph

From Wikipedia, the free encyclopedia

In the mathematical area of graph theory, a graph is even-hole-free if it contains no induced cycle with an even number of vertices.

Addario-Berry et al. (2008) demonstrated that every even-hole-free graph contains a bisimplicial vertex, which settled a conjecture by Reed.

Recognition

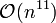Conforti et al. (2002) gave the first polynomial time recognition algorithm for even-hole-free graphs, which runs in ${{\mathcal O}}(n^{{40}})$ time.^[1] da Silva & Vušković (2008) later improved this to ${{\mathcal O}}(n^{{19}})$ . The best currently known algorithm is given by Chang & Lu (2011) which runs in time ${{\mathcal O}}(n^{{11}})$ .

While even-hole-free graphs can be recognized in polynomial time, it is NP-complete to determine whether a graph contains an even hole that includes a specific vertex.^[2]

Notes

↑ Conforti et al. (2002) present their algorithm and assert that it runs in polynomial time without giving an explicit analysis. Chudnovsky, Kawarabayashi & Seymour (2004) estimate that it runs in "time about ${{\mathcal O}}(n^{{40}})$ ."
↑ Bienstock (1991)

References

Addario-Berry, Louigi; Chudnovsky, Maria; Havet, Frédéric; Reed, Bruce; Seymour, Paul (2008), "Bisimplicial vertices in even-hole-free graphs", Journal of Combinatorial Theory, Series B 98 (6): 1119–1164, doi:10.1016/j.jctb.2007.12.006

Bienstock, Dan (1991), "On the complexity of testing for odd holes and induced odd paths", Discrete Mathematics 90 (1): 85–92, doi:10.1016/0012-365X(91)90098-M

Chudnovsky, Maria; Kawarabayashi, Ken-ichi; Seymour, Paul (2004), "Detecting even holes", Journal of Graph Theory 48 (2): 85–111, doi:10.1002/jgt.20040

Conforti, Michele; Cornuéjols, Gérard; Kapoor, Ajai; Vušković, Kristina (2002), "Even-hole-free graphs part I: Decomposition theorem", Journal of Graph Theory 39 (1): 6–49, doi:10.1002/jgt.10006

Conforti, Michele; Cornuéjols, Gérard; Kapoor, Ajai; Vušković, Kristina (2002), "Even-hole-free graphs part II: Recognition algorithm", Journal of Graph Theory 40 (4): 238–266, doi:10.1002/jgt.10045

da Silva, Murilo V.G.; Vušković, Kristina, Decomposition of even-hole-free graphs with star cutsets and 2-joins

Chang, Hsien-Chih; Lu, Hsueh-I, A Faster Algorithm to Recognize Even-Hole-Free Graphs

External links

"Graphclass: even-cycle-free". Information System on Graph Classes and their Inclusions.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.