Eulerian matroid
In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.
Examples
In a uniform matroid 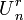 , the circuits are the sets of exactly
, the circuits are the sets of exactly 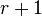 elements. Therefore, a uniform matroid is Eulerian if and only if
elements. Therefore, a uniform matroid is Eulerian if and only if 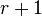 is a divisor of
is a divisor of  . For instance, the
. For instance, the  -point lines
-point lines 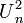 are Eulerian if and only if
are Eulerian if and only if  is divisible by three.
is divisible by three.
The Fano plane has two kinds of circuits: sets of three collinear points, and sets of four points that do not contain any line. The three-point circuits are the complements of the four-point circuits, so it is possible to partition the seven points of the plane into two circuits, one of each kind. Thus, the Fano plane is also Eulerian.
Relation to Eulerian graphs
Eulerian matroids were defined by Welsh (1969) as a generalization of the Eulerian graphs, graphs in which every vertex has even degree. By Veblen's theorem the edges of every such graph may be partitioned into simple cycles, from which it follows that the graphic matroids of Eulerian graphs are examples of Eulerian matroids.[1]
The definition of an Eulerian graph above allows graphs that are disconnected, so not every such graph has an Euler tour. Wilde (1975) observes that the graphs that have Euler tours can be characterized in an alternative way that generalizes to matroids: a graph  has an Euler tour if and only if it can be formed from some other graph
has an Euler tour if and only if it can be formed from some other graph 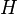 , and a cycle
, and a cycle  in
in 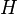 , by contracting the edges of
, by contracting the edges of 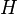 that do not belong to
that do not belong to  . In the contracted graph,
. In the contracted graph,  generally stops being a simple cycle and becomes instead an Euler tour. Analogously, Wilde considers the matroids that can be formed from a larger matroid by contracting the elements that do not belong to some particular circuit. He shows that this property is trivial for general matroids (it implies only that each element belongs to at least one circuit) but can be used to characterize the Eulerian matroids among the binary matroids, matroids representable over GF(2):
a binary matroid is Eulerian if and only if it is the contraction of another binary matroid onto a circuit.[2]
generally stops being a simple cycle and becomes instead an Euler tour. Analogously, Wilde considers the matroids that can be formed from a larger matroid by contracting the elements that do not belong to some particular circuit. He shows that this property is trivial for general matroids (it implies only that each element belongs to at least one circuit) but can be used to characterize the Eulerian matroids among the binary matroids, matroids representable over GF(2):
a binary matroid is Eulerian if and only if it is the contraction of another binary matroid onto a circuit.[2]
Duality with bipartite matroids
For planar graphs, the properties of being Eulerian and bipartite are dual: a planar graph is Eulerian if and only if its dual graph is bipartite. As Welsh showed, this duality extends to binary matroids: a binary matroid is Eulerian if and only if its dual matroid is a bipartite matroid, a matroid in which every circuit has even cardinality.[1][3]
For matroids that are not binary, the duality between Eulerian and bipartite matroids may break down. For instance, the uniform matroid 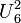 is Eulerian but its dual
is Eulerian but its dual 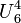 is not bipartite, as its circuits have size five. The self-dual uniform matroid
is not bipartite, as its circuits have size five. The self-dual uniform matroid  is bipartite but not Eulerian.
is bipartite but not Eulerian.
Alternative characterizations
Because of the correspondence between Eulerian and bipartite matroids among the binary matroids, the binary matroids that are Eulerian may be characterized in alternative ways. The characterization of Wilde (1975) is one example; two more are that a binary matroid is Eulerian if and only if every element belongs to an odd number of circuits, if and only if the whole matroid has an odd number of partitions into circuits.[4] Lovász & Seress (1993) collect several additional characterizations of Eulerian binary matroids, from which they derive a polynomial time algorithm for testing whether a binary matroid is Eulerian.[5]
Computational complexity
Any algorithm that tests whether a given matroid is Eulerian, given access to the matroid via an independence oracle, must perform an exponential number of oracle queries, and therefore cannot take polynomial time.[6]
Eulerian extension
If  is a binary matroid that is not Eulerian, then it has a unique Eulerian extension, a binary matroid
is a binary matroid that is not Eulerian, then it has a unique Eulerian extension, a binary matroid 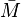 whose elements are the elements of
whose elements are the elements of  together with one additional element
together with one additional element  , such that the restriction of
, such that the restriction of 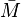 to the elements of
to the elements of  is isomorphic to
is isomorphic to  . The dual of
. The dual of 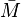 is a bipartite matroid formed from the dual of
is a bipartite matroid formed from the dual of  by adding
by adding  to every odd circuit.[7]
to every odd circuit.[7]
References
- ↑ 1.0 1.1 Welsh, D. J. A. (1969), "Euler and bipartite matroids", Journal of Combinatorial Theory 6: 375–377, MR 0237368.
- ↑ Wilde, P. J. (1975), "The Euler circuit theorem for binary matroids", Journal of Combinatorial Theory, Series B 18: 260–264, MR 0384577.
- ↑ Harary, Frank; Welsh, Dominic (1969), "Matroids versus graphs", The Many Facets of Graph Theory (Proc. Conf., Western Mich. Univ., Kalamazoo, Mich., 1968), Lecture Notes in Mathematics 110, Berlin: Springer, pp. 155–170, doi:10.1007/BFb0060114, MR 0263666.
- ↑ Shikare, M. M. (2001), "New characterizations of Eulerian and bipartite binary matroids", Indian Journal of Pure and Applied Mathematics 32 (2): 215–219, MR 1820861.
- ↑ Lovász, László; Seress, Ákos (1993), "The cocycle lattice of binary matroids", European Journal of Combinatorics 14 (3): 241–250, doi:10.1006/eujc.1993.1027, MR 1215334.
- ↑ Jensen, Per M.; Korte, Bernhard (1982), "Complexity of matroid property algorithms", SIAM Journal on Computing 11 (1): 184–190, doi:10.1137/0211014, MR 646772.
- ↑ Sebő, András (1990), "The cographic multiflow problem: an epilogue", Polyhedral combinatorics (Morristown, NJ, 1989), DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 1, Providence, RI: Amer. Math. Soc., pp. 203–234, MR 1105128.