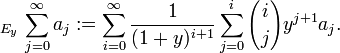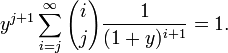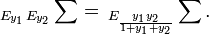Euler summation

From Wikipedia, the free encyclopedia

In the mathematics of convergent and divergent series, Euler summation is a summability method. That is, it is a method for assigning a value to a series, different from the conventional method of taking limits of partial sums. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series. As well as being used to define values for divergent series, Euler summation can be used to speed the convergence of series.

Euler summation can be generalized into a family of methods denoted (E, q), where q ≥ 0. The (E, 0) sum is the usual (convergent) sum, while (E, 1) is the ordinary Euler sum. All of these methods are strictly weaker than Borel summation; for q > 0 they are incomparable with Abel summation.

Definition

Euler summation is particularly used to accelerate the convergence of alternating series and allows evaluating divergent sums.

_{{E_{y}}}\,\sum _{{j=0}}^{\infty }a_{j}:=\sum _{{i=0}}^{\infty }{\frac {1}{(1+y)^{{i+1}}}}\sum _{{j=0}}^{i}{i \choose j}y^{{j+1}}a_{j}.

To justify the approach notice that for interchanged sum, Euler's summation reduces to the initial series, because

y^{{j+1}}\sum _{{i=j}}^{\infty }{i \choose j}{\frac {1}{(1+y)^{{i+1}}}}=1.

This method itself cannot be improved by iterated application, as

_{{E_{{y_{1}}}}}{}_{{E_{{y_{2}}}}}\sum =\,_{{E_{{{\frac {y_{1}y_{2}}{1+y_{1}+y_{2}}}}}}}\sum .

Examples

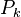  • We have \sum _{{j=0}}^{\infty }x^{j}P_{k}(j)=\sum _{{i=0}}^{k}{\frac {x^{i}}{(1-x)^{{i+1}}}}\sum _{{j=0}}^{i}{i \choose j}(-1)^{{i-j}}P_{k}(j), if P_{k} is a polynomial of degree k. Note that in this case Euler summation reduces an infinite series to a finite sum.
  • The particular choice P_{k}(j):=(j+1)^{k} provides an explicit representation of the Bernoulli numbers, since \zeta (-k)=-{\frac {B_{{k+1}}}{k+1}}. Indeed, applying Euler summation to the zeta function yields {\frac {1}{1-2^{{k+1}}}}\sum _{{i=0}}^{k}{\frac {1}{2^{{i+1}}}}\sum _{{j=0}}^{i}{i \choose j}(-1)^{j}(j+1)^{k}, which is polynomial for k a positive integer; cf. Riemann zeta function.
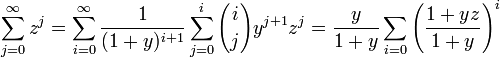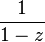  • \sum _{{j=0}}^{\infty }z^{j}=\sum _{{i=0}}^{\infty }{\frac {1}{(1+y)^{{i+1}}}}\sum _{{j=0}}^{i}{i \choose j}y^{{j+1}}z^{j}={\frac {y}{1+y}}\sum _{{i=0}}\left({\frac {1+yz}{1+y}}\right)^{i}. With an appropriate choice of y this series converges to {\frac {1}{1-z}}.

See also

References

  • Korevaar, Jacob (2004). Tauberian Theory: A Century of Developments. Springer. ISBN 3-540-21058-X. 
  • Shawyer, Bruce and Bruce Watson (1994). Borel's Methods of Summability: Theory and Applications. Oxford UP. ISBN 0-19-853585-6. 
  • Apostol, Tom M. (1974). Mathematical Analysis Second Edition. Addison Wesley Longman. ISBN 0-201-00288-4. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.