Euclidean field
From Wikipedia, the free encyclopedia
For algebraic number fields whose ring of integers has a Euclidean algorithm, see Euclidean domain.
In mathematics, a Euclidean field is an ordered field K for which every non-negative element is a square: that is, x ≥ 0 in K implies that x = y2 for some y in K.
Properties
- Every Euclidean field is an ordered Pythagorean field, but the converse is not true.[1]
- If E/F is a finite extension, and E is Euclidean, then so is F. This "going-down theorem" is a consequence of the Diller–Dress theorem.[2]
Examples
- The real numbers R with the usual operations and ordering form a Euclidean field.
- The field of real algebraic numbers
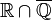 is a Euclidean field.
is a Euclidean field. - The real constructible numbers, those (signed) lengths which can be constructed from a rational segment by ruler and compass constructions, form a Euclidean field.[3]
- The field of hyperreal numbers is a Euclidean field.
Counterexamples
- The rational numbers Q with the usual operations and ordering do not form a Euclidean field. For example, 2 is not a square in Q since the square root of 2 is irrational.[4] By the going-down result above, no algebraic number field can be Euclidean.[2]
- The complex numbers C do not form a Euclidean field since they cannot be given the structure of an ordered field.
Euclidean closure
The Euclidean closure of an ordered field K is a maximal extension of K in the quadratic closure of K which is again an ordered field with an order extending that of K.[5]
References
- Efrat, Ido (2006). Valuations, orderings, and Milnor K-theory. Mathematical Surveys and Monographs 124. Providence, RI: American Mathematical Society. ISBN 0-8218-4041-X. Zbl 1103.12002.
- Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.
- Martin, George E. (1998). Geometric Constructions. Undergraduate Texts in Mathematics. Springer-Verlag. ISBN 0-387-98276-0.
External links
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.