Ergodic process
In econometrics and signal processing, a stochastic process is said to be ergodic if its statistical properties (such as its mean and variance) can be deduced from a single, sufficiently long sample (realization) of the process.
Specific definitions
One can discuss the ergodicity of various properties of a stochastic process. For example, a wide-sense stationary process  has mean
has mean ![m_{x}(t)=E[x(t)]](/2014-wikipedia_en_all_02_2014/I/media/d/7/5/d/d75d6eab6d2458615fc0134aa2b12ae7.png) and autocovariance
and autocovariance ![r_{x}(\tau )=E[(x(t)-m_{x}(t))(x(t+\tau )-m_{x}(t+\tau ))]](/2014-wikipedia_en_all_02_2014/I/media/0/0/7/7/0077d138c0195cb2e0f71a2957cddb92.png) which do not change with time. One way to estimate the mean is to perform a time average:
which do not change with time. One way to estimate the mean is to perform a time average:
If  converges in squared mean to
converges in squared mean to 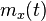 as
as 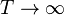 , then the process
, then the process  is said to be mean-ergodic[1] or mean-square ergodic in the first moment.[2]
is said to be mean-ergodic[1] or mean-square ergodic in the first moment.[2]
Likewise, one can estimate the autocovariance 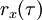 by performing a time average:
by performing a time average:
If this expression converges in squared mean to the true autocovariance ![r_{x}(\tau )=E[(x(t+\tau )-m_{x}(t+\tau ))(x(t)-m_{x}(t))]](/2014-wikipedia_en_all_02_2014/I/media/e/d/2/1/ed21454626944ab8077b289e97c3db51.png) , then the process is said to be autocovariance-ergodic or mean-square ergodic in the second moment.[2]
, then the process is said to be autocovariance-ergodic or mean-square ergodic in the second moment.[2]
A process which is ergodic in the first and second moments is sometimes called ergodic in the wide sense.[2]
An important example of an ergodic processes is the stationary Gaussian process with continuous spectrum.
See also
- Poincaré recurrence theorem
- Loschmidt's paradox
- Ergodic theory, a branch of mathematics concerned with a more general formulation of ergodicity
- Ergodic hypothesis
- Ergodicity
Notes
References
- Porat, B. (1994). Digital Processing of Random Signals: Theory & Methods. Prentice Hall. p. 14. ISBN 0-13-063751-3.
- Papoulis, Athanasios (1991). Probability, random variables, and stochastic processes. New York: McGraw-Hill. pp. 427–442. ISBN 0-07-048477-5.

![{\hat {r}}_{x}(\tau )={\frac {1}{2T}}\int _{{-T}}^{{T}}[x(t+\tau )-m_{x}(t+\tau )][x(t)-m_{x}(t)]\,dt.](/2014-wikipedia_en_all_02_2014/I/media/8/3/c/d/83cd6127830d6696706a6073d311a390.png)