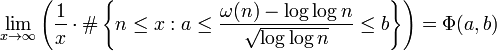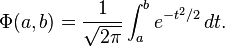Erdős–Kac theorem

From Wikipedia, the free encyclopedia

In number theory, the Erdős–Kac theorem, named after Paul Erdős and Mark Kac, and also known as the fundamental theorem of probabilistic number theory, states that if ω(n) is the number of distinct prime factors of n, then, loosely speaking, the probability distribution of

${\frac {\omega (n)-\log \log n}{{\sqrt {\log \log n}}}}$

is the standard normal distribution. This is a deep extension of the Hardy–Ramanujan theorem, which states that the normal order of ω(n) is log log n with a typical error of size 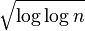${\sqrt {\log \log n}}$ .

More precisely, for any fixed a < b,

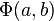$\lim _{{x\rightarrow \infty }}\left({\frac {1}{x}}\cdot \#\left\{n\leq x:a\leq {\frac {\omega (n)-\log \log n}{{\sqrt {\log \log n}}}}\leq b\right\}\right)=\Phi (a,b)$

where $\Phi (a,b)$ is the normal (or "Gaussian") distribution, defined as

$\Phi (a,b)={\frac {1}{{\sqrt {2\pi }}}}\int _{a}^{b}e^{{-t^{2}/2}}\,dt.$

Stated somewhat heuristically, what Erdős and Kac proved was that if n is a randomly chosen large integer, then the number of distinct prime factors of n has approximately the normal distribution with mean and variance log log n.

This means that the construction of a number around one billion requires on average three primes.

For example 1,000,000,003 = 23 × 307 × 141623.

n	Number of Digits in n	Average number of distinct primes	standard deviation
1,000	4	2	1.4
1,000,000,000	10	3	1.7
1,000,000,000,000,000,000,000,000	25	4	2
10⁶⁵	66	5	2.2
10^9,566	9,567	10	3.2
10^210,704,568	210,704,569	20	4.5
10^10²²	10²²+1	50	7.1
10^10⁴⁴	10⁴⁴+1	100	10
10^10⁴³⁴	10⁴³⁴+1	1000	31.6

A spreading Gaussian distribution of distinct primes illustrating the Erdos-Kac theorem

Around 12.6% of 10,000 digit numbers are constructed from 10 distinct prime numbers and around 68% (±σ) are constructed from between 7 and 13 primes.

A hollow sphere the size of the planet Earth filled with fine sand would have around 10³³ grains. A volume the size of the observable universe would have around 10⁹³ grains of sand. There might be room for 10¹⁸⁵ quantum strings in such a universe.

Numbers of this magnitude—with 186 digits—would require on average only 6 primes for construction.

References

Erdős, Paul; Kac, Mark (1940). "The Gaussian Law of Errors in the Theory of Additive Number Theoretic Functions". American Journal of Mathematics 62 (1/4): 738–742. ISSN 0002-9327. Zbl 0024.10203.
Kuo, Wentang; Liu, Yu-Ru (2008). "The Erdős–Kac theorem and its generalizations". In De Koninck, Jean-Marie; Granville, Andrew; Luca, Florian. Anatomy of integers. Based on the CRM workshop, Montreal, Canada, March 13--17, 2006. CRM Proceedings and Lecture Notes 46. Providence, RI: American Mathematical Society. pp. 209–216. ISBN 978-0-8218-4406-9. Zbl 1187.11024.
Kac, Mark (1959). Statistical Independence in Probability, Analysis and Number Theory. John Wiley and Sons, Inc.

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.