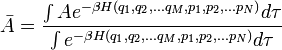Ensemble average

From Wikipedia, the free encyclopedia

Canonical ensemble average

Classical statistical mechanics

For a classical system in thermal equilibrium with its environment, the ensemble average takes the form of an integral over the phase space of the system:

${\bar {A}}={\frac {\int {Ae^{{-\beta H(q_{1},q_{2},...q_{M},p_{1},p_{2},...p_{N})}}d\tau }}{\int {e^{{-\beta H(q_{1},q_{2},...q_{M},p_{1},p_{2},...p_{N})}}d\tau }}}$

where:

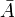${\bar {A}}$ is the ensemble average of the system property A,

$\beta$ is ${\frac {1}{kT}}$ , known as thermodynamic beta,

H is the Hamiltonian of the classical system in terms of the set of coordinates $q_{i}$ and their conjugate generalized momenta $p_{i}$ , and

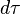$d\tau$ is the volume element of the classical phase space of interest.

The denominator in this expression is known as the partition function, and is denoted by the letter Z.

Quantum statistical mechanics

For a quantum system in thermal equilibrium with its environment, the weighted average takes the form of a sum over quantum energy states, rather than a continuous integral:

Characterization of the classical limit

Ensemble average in other ensembles

The generalized version of the partition function provides the complete framework for working with ensemble averages in thermodynamics, information theory, statistical mechanics and quantum mechanics.

Microcanonical Ensemble

Macrocanonical ensemble

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.