Energy landscape

From Wikipedia, the free encyclopedia

In physics and biochemistry, an energy landscape is a mapping of all possible conformations of a molecular entity, or the spatial positions of interacting molecules in a system, and their corresponding energy levels, typically Gibbs free energy.

The term is useful when examining protein folding; while a protein can theoretically exist in a nearly infinite number of conformations along its energy landscape, in reality proteins fold (or "relax") into secondary and tertiary structures that possess the lowest possible free energy. The key concept in the energy landscape approach to protein folding is the folding funnel hypothesis.

In glassing models, the local minima of an energy landscape correspond to metastable low temperature states of a thermodynamic system.[1]

Formal definition

Mathematically, an energy landscape is a continuous function f:X\to {\mathbb {R}} associating each physical state with an energy, where X is a topological space.

In the continuous case, 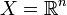X={\mathbb {R}}^{n}, where n is the number of degrees of freedom of the system. The graph of a continuous energy landscape is a hypersurface in 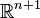{\mathbb {R}}^{{n+1}}.

Hills and valleys in the energy landscape correspond to local maxima and minima of f, respectively.

Macroscopic example

A well-oiled door hinge has one degree of freedom, so its energy landscape is a function f:{\mathbb {R}}\to {\mathbb {R}}. If the door hinge isn't mounted perfectly, the door will naturally swing closed, open, or to some partially open angle when it is allowed to swing freely. These angles correspond to states of minimal energy of the system, or valleys in the energy landscape.

See also

References

  1. ↑ Wales, David J. (2003). Energy Landscapes. Cambridge University Press. p. 68. ISBN 0-521-81415-4. 



This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.