End extension

From Wikipedia, the free encyclopedia

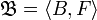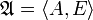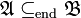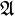In model theory and set theory, which are disciplines within mathematics, a model ${\mathfrak {B}}=\langle B,F\rangle$ of some axiom system of set theory $T\,$ in the language of set theory is an end extension of ${\mathfrak {A}}=\langle A,E\rangle$ , in symbols ${\mathfrak {A}}\subseteq _{{\text{end}}}{\mathfrak {B}}$ , if

${\mathfrak {A}}$ is a substructure of 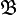${\mathfrak {B}}$ , and
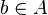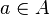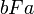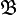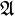$b\in A$ whenever $a\in A$ and $bFa\,$ hold, i.e., no new elements are added by ${\mathfrak {B}}$ to the elements of ${\mathfrak {A}}$ .

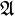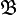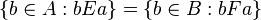The following is an equivalent definition of end extension: ${\mathfrak {A}}$ is a substructure of ${\mathfrak {B}}$ , and $\{b\in A:bEa\}=\{b\in B:bFa\}$ for all $a\in A$ .

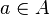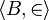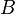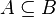For example, $\langle B,\in \rangle$ is an end extension of $\langle A,\in \rangle$ if $A\,$ and $B\,$ are transitive sets, and $A\subseteq B$ .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.