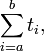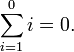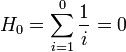Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero. For summations defined in terms of addition of other values than numbers (such as vectors, matrices, polynomials), in general of values in some given Abelian group, the value of an empty summation is taken to be the zero element of that group.
An empty sum can arise in particular for expressions of the form
when 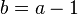 ; in such case the summation has value 0 (or the zero element of the additive group in which the terms ti live).
; in such case the summation has value 0 (or the zero element of the additive group in which the terms ti live).
A situation similar to an empty summation can arise for other operations than addition; notably, its counterpart for multiplication is an empty product, a product of no factors at all. In such cases the convention of a zero result does not apply; indeed the value of an empty product of numbers is taken to be one, the neutral element for multiplication.
Summation convention
Empty sums, or even sums of a single term, do not play a role in the definition of addition, since that operation requires exactly two operands. The need to consider empty sums arises with summation: the process of "adding together" a collection of values that can have an arbitrary size. For a finite collection of two or more numbers, the commutative and associative laws of addition imply that every expression formed using addition only, and in which all members of the collection appear exactly once as operand, has the same value; this defines the sum of the collection. For infinite collections of values this definition does not apply, as no (finite) expression can combine them all using addition operations; the notion of a series can be used to attach a definite sum to some infinite collections, but this requires more than addition only, notably some notion of limit.
This leaves the cases of collections with less than two elements. One could decide to leave the sum of such collections undefined, on the grounds that there are too few values to perform any addition. For various reasons it is however useful to not make such an exception, and define the sum of any finite collection of values. Doing so should be done without invalidating the usual properties of summation, notably the fact that adjoining a new value x to a collection adds x to the sum of the collection. This property then implies that the sum of a collection containing a single value v is v, and that the sum of a collection of no values at all is 0, the neutral element for addition. An alternative approach is to define the sum of a finite sequence of values by induction on its length, with as starting case the empty sequence whose sum is 0. Both approaches define the same notion of sum, and the latter does so without making any separate definition for an empty sum.
Relevance of defining empty sums
The necessity to define a value for empty summations is not immediately obvious, as it may appear strange to set up a summation when there is nothing to add. However empty summations often arise implicitly when the range of values being added depends on certain unknown parameters, and may become empty for certain values of the parameters. Leaving the value of an empty summation undefined would make it hard to make certain definitions properly, requiring frequent consideration of special cases to avoid empty sums. It would also imply an additional effort required in the proof of any statement involving summations to ensure that they never involve empty summations. In fact the reasons for defining empty sums are very similar to the reasons to considering things like the number zero and the empty set in the first place: while they seem to represent quite uninteresting notions, their existence allows for a much cleaner mathematical presentation of many subjects.
An even stronger case for the definition of empty sums arises when certain notions are defined in terms of the existence of summations; not defining empty sums would implicitly alter such notions in a way that is usually undesirable. For instance in number theory, a partition of an integer n can be defined as a weakly decreasing sequence of positive integers whose sum is n. It is important that there is exactly one partition of the number 0 (most formulas for counting partitions would break down if there were assumed to be no partitions of 0), and since terms must be positive, the empty sequence is the only possible candidate. More generally, it often happens in combinatorics that certain values are considered to be a member of a given class by virtue of an empty sum, for instance 0 is a triangular number because of
An example: empty linear combinations
Outside combinatorics, additive decompositions occur less frequently than multiplicative ones, which makes this kind of argument for defining empty sums less obvious than similar arguments for empty products. However linear algebra does provide one such example in the form of empty linear combinations. One characterization of a linearly dependent set is that one of its elements can be written as a linear combination of the other elements; if this is to apply to the linearly dependent set containing just the zero vector, it must be that the zero vector is a linear combination of no vectors at all, which is an empty sum of vectors. Also every finite dimensional vector space admits a basis, whose number of elements is equal to the dimension, and every element of the vector space can be uniquely expressed as linear combination of basis vectors. Applying this to a space of dimension 0, which contains exactly one vector (the zero vector), the only candidate for a basis is the empty set (both because 0 elements are required, and because the zero vector cannot be in any basis). Then the zero vector of this space can be expressed as a linear combination of no elements, which again is an empty sum.
Significance of "terms" of an empty sum
Since an empty sum by definition has no terms, it seems contradictory to talk about its terms; however in practice there almost always is an expression that describes the terms of a summation, even if the range of summation happens to be empty. Since this expression is never instantiated in an empty sum, its value is irrelevant; for instance the harmonic number
is perfectly well defined. However, the kind of values denoted by the summand is of importance for the value of the summation; for instance, an empty summation of elements of a vector space has as value the zero vector in that space, rather than the number 0. Even more important is the fact that the operation is summation; by contrast, the empty product—a product of no factors at all—has a value of one.
See also
References
- A. E. Ingham, contributor R. C. Vaughan, The Distribution of Prime Numbers, Cambridge University Press, 1990, ISBN 0-521-39789-8