Elongated triangular gyrobicupola

From Wikipedia, the free encyclopedia

Elongated triangular gyrobicupola

Type	Johnson J₃₅ - J₃₆ - J₃₇
Faces	2+6 triangles 2.6 squares
Edges	36
Vertices	18
Vertex configuration	6(3.4.3.4) 12(3.4³)
Symmetry group	D_3d
Dual polyhedron	-
Properties	convex
Net

In geometry, the elongated triangular gyrobicupola is one of the Johnson solids (J₃₆). As the name suggests, it can be constructed by elongating a "triangular gyrobicupola," or cuboctahedron, by inserting a hexagonal prism between its two halves, which are congruent triangular cupolae (J₃). Rotating one of the cupolae through 60 degrees before the elongation yields the triangular orthobicupola (J₃₅).

A Johnson solid is one of 92 strictly convex regular-faced polyhedra, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. They are named by Norman Johnson who first enumerated the set in 1966.

Formulae

The following formulae for volume and surface area can be used if all faces are regular, with edge length a:^[1]

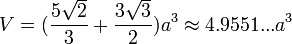
$V=({\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}})a^{3}\approx 4.9551...a^{3}$

$A=2(6+{\sqrt {3}})a^{2}\approx 15.4641...a^{2}$

References

↑ Stephen Wolfram, "Elongated triangular gyrobicupola" from Wolfram Alpha. Retrieved July 25, 2010.

External links

Weisstein, Eric W., "Johnson solid", MathWorld.
Weisstein, Eric W., "Elongated triangular gyrobicupola", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.