Elementary abelian group

From Wikipedia, the free encyclopedia

In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; it is a particular kind of p-group.

By the classification of finitely generated abelian groups, every elementary abelian group must be of the form

(Z/pZ)n

for n a non-negative integer (sometimes called the group's rank). Here, Z/pZ denotes the cyclic group of order p (or equivalently the integers mod p), and the notation means the n-fold Cartesian product.

Examples and properties

  • The elementary abelian group (Z/2Z)2 has four elements: { (0,0), (0,1), (1,0), (1,1) }. Addition is performed componentwise, taking the result mod 2. For instance, (1,0) + (1,1) = (0,1).
  • (Z/pZ)n is generated by n elements, and n is the least possible number of generators. In particular, the set {e1, ..., en}, where ei has a 1 in the ith component and 0 elsewhere, is a minimal generating set.
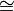(Z/pZ)n \cong < e1, ..., en | eip = 1, eiej = ejei >

Vector space structure

Suppose V 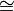\cong (Z/pZ)n is an elementary abelian group. Since Z/pZ 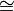\cong Fp, the finite field of p elements, we have V = (Z/pZ)n 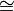\cong Fpn, hence V can be considered as an n-dimensional vector space over the field Fp. Note that an elementary abelian group does not in general have a distinguished basis: choice of isomorphism V 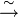{\overset {\sim }{\to }} (Z/pZ)n corresponds to a choice of basis.

To the observant reader, it may appear that Fpn has more structure than the group V, in particular that it has scalar multiplication in addition to (vector/group) addition. However, V as an abelian group has a unique Z-module structure where the action of Z corresponds to repeated addition, and this Z-module structure is consistent with the Fp scalar multiplication. That is, c·g = g + g + ... + g (c times) where c in Fp (considered as an integer with 0 ≤ c < p) gives V a natural Fp-module structure.

Automorphism group

As a vector space V has a basis {e1, ..., en} as described in the examples. If we take {v1, ..., vn} to be any n elements of V, then by linear algebra we have that the mapping T(ei) = vi extends uniquely to a linear transformation of V. Each such T can be considered as a group homomorphism from V to V (an endomorphism) and likewise any endomorphism of V can be considered as a linear transformation of V as a vector space.

If we restrict our attention to automorphisms of V we have Aut(V) = { T : V → V | ker T = 0 } = GLn(Fp), the general linear group of n × n invertible matrices on Fp.

A generalisation to higher orders

It can also be of interest to go beyond prime order components to prime-power order. Consider an elementary abelian group G to be of type (p,p,...,p) for some prime p. A homocyclic group[1] (of rank n) is an abelian group of type (pe,pe,...,pe) i.e. the direct product of n isomorphic groups of order pe.

Related groups

The extra special groups are extensions of elementary abelian groups by a cyclic group of order p, and are analogous to the Heisenberg group.

References

  1. ↑ Gorenstein, Daniel (1968). "1.2". Finite Groups. New York: Harper & Row. p. 8. ISBN 0-8218-4342-7. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.