Elasticity of complementarity

From Wikipedia, the free encyclopedia

Elasticity of complementarity (Hamermesh, 1993) is the percentage responsiveness of relative factor prices to a 1 percent change in relative inputs.

Mathematical definition

Given the production function 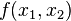$f(x_{1},x_{2})$ then the elasticity of complementarity is defined as

$c={\frac {d\ln \left(\displaystyle {\frac {df}{dx_{1}}}/\displaystyle {\frac {df}{dx_{2}}}\right)}{d\ln(x_{2}/x_{1})}}={\frac {\displaystyle {\frac {d({\frac {df}{dx_{1}}}/{\frac {df}{dx_{2}}})}{{\frac {df}{dx_{1}}}/{\frac {df}{dx_{2}}}}}}{\displaystyle {\frac {d(x_{2}/x_{1})}{x_{2}/x_{1}}}}}.$

The inverse of elasticity of complementarity is elasticity of substitution.

References

Hamermesh, Daniel S., Labor Demand, Princeton University Press, Princeton NJ, 1993, ISBN 0-691-02587-8

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.